最短路径-Floyed和Dijkstra

最短路径-Floyed和Dijkstra

Floyed

样题一：P1364 医院设置

题目描述：

设有一棵二叉树，如图：

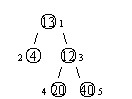
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 11。如上图中，若医院建在1 处，则距离和 =4+12+2\times20+2\times40=136=4+12+2×20+2×40=136；若医院建在 33 处，则距离和 =4\times2+13+20+40=81=4×2+13+20+40=81。

输入格式：

第一行一个整数 nn，表示树的结点数。

接下来的 nn 行每行描述了一个结点的状况，包含三个整数 w, u, vw,u,v，其中 ww 为居民人口数，uu 为左链接（为 00 表示无链接），vv 为右链接（为 00 表示无链接）。

输出格式：

一个整数，表示最小距离和。

输入输出样例：

1
2
3
4
5
6
5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出：

1
81

程序源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <bits/stdc++.h>
using namespace std;
int tree[1000][1000];   //tree的作用邻接矩阵建树
int w[1000],l,r;  //w每个结点的居民人口数
int mindis;       //最小记录和
int main() {
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            tree[i][j]=0X3FFFFFFF;    //初始化邻接矩阵
        }
    }
    for (int i = 1; i <=n ; ++i) {
        tree[i][i]=0;    //初始化
        cin>>w[i]>>l>>r;  //读入数据
        if(l>0) tree[i][l]=tree[l][i]=1;
        if(r>0) tree[i][r]=tree[r][i]=1;
    }
    for (int k = 1; k <=n ; ++k) //用Floyed求任意两结点之间的最短路径
    {
        for (int i = 1; i <=n ; ++i) {
            if(i!=k)
            {
                for (int j = 1; j <=n ; ++j) {
                    if(i!=j&&j!=k&&tree[i][k]+tree[k][j]<tree[i][j])
                    {
                        tree[i][j]=tree[i][k]+tree[k][j];
                    }
                }
            }
        }
    }
    mindis=INT_MAX;
    for(int i=1;i<=n;i++) //穷举医院建在N个结点，找出最短距离
    {
        int sum =0;
        for(int j=1;j<=n;j++)
        {
            sum+=tree[i][j]*w[j];
        }
        if(sum<mindis) mindis=sum;
    }
    cout<<mindis<<endl;
    return 0;
}

Dijkstra

样题二：

题目描述：

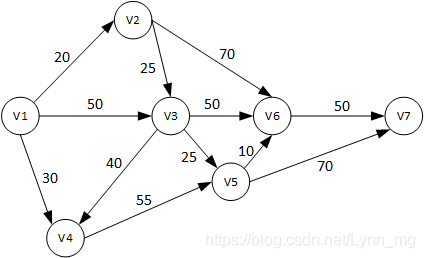
输入n和m，代表n个节点，m条边，然后是m行输入，每行有x,y,z，代表x到y的路距离为z。
问题：从1出发到各点的最短路径

测试样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
7 12
1 2 20
1 3 50
1 4 30
2 3 25
2 6 70
3 4 40
3 6 50
3 5 25
4 5 55
5 6 10
5 7 70
6 7 50
5

输出：

1
2
1->2->3->5
70

程序源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100;
int mapdis[maxn][maxn];  //表示x->y的距离(有向)
int dis[maxn];  //代表最短路径长
int path[maxn];  //记录前驱节点
int vis[maxn]; //用来记录该点是否已经是最短路径的点
int n,m;
void Dijkstra(int s)
{
    //初始化
    memset(dis,0x3f,sizeof(dis));
    memset(path,-1,sizeof(path));
    memset(vis,0,sizeof(vis));
    
    dis[s]=0;   //自身到自身的距离是0
    while(1)
    {
        int k=0; //用来记录当轮的起始点
        for (int i = 1; i <=n; ++i) {
            if(!vis[i]&&dis[i]<dis[k])     //如果这个点还不为最短路径的点，并且这个点的路径是现在所有点中最小的
            {
                k=i;      //那么就记录这个点为当轮的起始点
                		  //特殊的这里第一次找到的是起点，及s=1。
            }
        }
        if(!k) return;  //所有点已经为最短路径的点，则返回
        vis[k]=1;       //标记该点为最短路径的点
        //松弛操作
        for (int j = 1; j <=n ; ++j) {   
            //第一次循环只有起点的邻接点的距离被更新
            //每次都更新找到，新找到的点的邻接点(新找到的点也就是当轮的起始点)
            if(dis[j]>dis[k]+mapdis[k][j])  //最短路是由最短路+某一条固定路组成
            {
                dis[j]=dis[k]+mapdis[k][j];//路径被改变
                path[j]=k;//重新记录前驱，最短路是由最短路+某一条固定路组成，所以前驱是有效的
            }
        }

    }

}
void print(int x) //递归打印
{
    if(x == -1) return;
    print(path[x]);
    cout<<x<<"->";
}
int main() {
    n,m;
    cin>>n>>m;
    //初始化
    memset(mapdis,0x3f,sizeof(mapdis));
    for (int i = 0; i <m ; ++i) {
        int x,y,z;
        cin>>x>>y>>z;
        //记录x->y的距离
        mapdis[x][y]=z;
    }
    Dijkstra(1);  //求1出发到各点的最短路径
    int order;    //读入终点
    cin>>order;
    print(path[order]);  //打印最短路径
    cout<<order<<endl;
    cout<<dis[order];    //最短路径长
    return 0;
}

样题三：L2-001 紧急救援 (25 分)

题目描述：

作为一个城市的应急救援队伍的负责人，你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候，你的任务是带领你的救援队尽快赶往事发地，同时，一路上召集尽可能多的救援队。

输入格式:

输入第一行给出4个正整数N、M、S、D，其中N（2≤N≤500）是城市的个数，顺便假设城市的编号为0 ~ (N−1)；M是快速道路的条数；S是出发地的城市编号；D是目的地的城市编号。

第二行给出N个正整数，其中第i个数是第i个城市的救援队的数目，数字间以空格分隔。随后的M行中，每行给出一条快速道路的信息，分别是：城市1、城市2、快速道路的长度，中间用空格分开，数字均为整数且不超过500。输入保证救援可行且最优解唯一。

输出格式:

第一行输出最短路径的条数和能够召集的最多的救援队数量。第二行输出从S到D的路径中经过的城市编号。数字间以空格分隔，输出结尾不能有多余空格。

输入样例:

1
2
3
4
5
6
7
4 5 0 3
20 30 40 10
0 1 1
1 3 2
0 3 3
0 2 2
2 3 2结尾无空行

输出样例:

1
2
2 60
0 1 3结尾无空行

最短路径条数：

如果通过 index 点能把最短路径更新，那么最短路径条数就是从起点到index的最短路径条数。

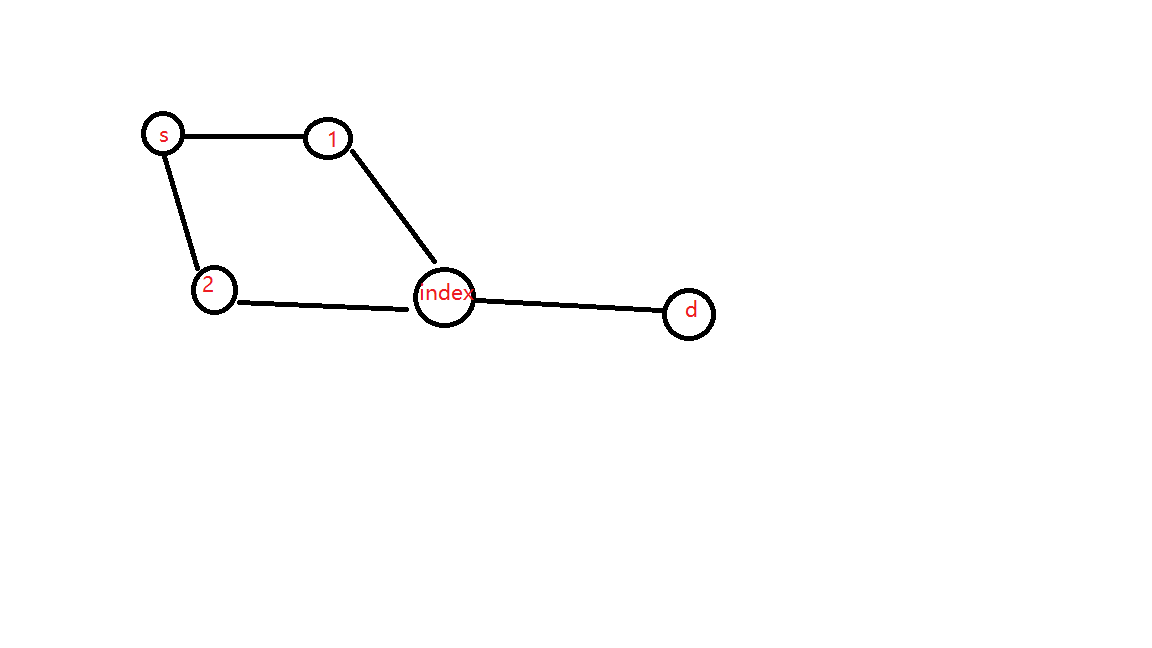
例如这张图，如果index可以更新当前的最短路径，并且s通过1和2到达index点的距离都相等，那么从s到d的最短路径条数其实就是从s到index的最短路径条数，由此可以得到第一个式子

1
num[i]=num[index];

如果通过index点的周转，距离不变（依然是最小值），这说明通过index周转使得最短路径条数又多出了一部分，只需要用之前得到的最短路径条数加上num[index]即可，由此得出第二个式子

1
num[i]+=num[index];

程序源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <bits/stdc++.h>
using namespace std;
int n,m,s,d;
const int maxn=505;
int arr[maxn];   //记录每个城市的援兵数
int dismap[maxn][maxn];    //储存X-Y的长度
int path[maxn];    //前驱节点
int dis[maxn];     //最短路径
int cost[maxn];    //最大救援队数量
int vis[maxn];     //用来记录该点是否已经是最短路径的点
int num[maxn];     //最短路径的条数
void dijk(int s)
{
    memset(path,-1,sizeof(path));
    memset(dis,0x3f,sizeof(dis));
    memset(cost,0,sizeof(cost));
    memset(vis,0,sizeof(vis));
    memset(num,0,sizeof(num));
    dis[s]=0;
    cost[s]=arr[s];   //此时救援队数量等于出发点的救援队数量
    num[s]=1;         //一条最短路径
    while(true)
    {
        int k=-1;
        int maxt =0x3f;
        for (int i = 0; i < n; ++i) {
            if(!vis[i]&&dis[i]<maxt)
            {
                k=i;
                maxt=dis[i];
            }
        }
        vis[k]=1;
        if(k==-1) return;

        for (int j = 0; j < n; ++j) {

            if(!vis[j]&&dis[j]>dis[k]+dismap[k][j]){
                dis[j]=dis[k]+dismap[k][j];
                path[j]=k;
                num[j]=num[k];   //如果能更新，说明产生了新的最短路径，num[i]变为从s到k的路径条数
                cost[j] = cost[k]+arr[j];  //产生了新的最短路径,人数为cost[k]+arr[j]
            }
            else if (!vis[j]&&dis[j]==dis[k]+dismap[k][j]){ //存在新的最短路径
                num[j]+=num[k];   //最短路径条数更新
                //无论援兵量是否能更新，既然已经有了另一条路与当前最短路长度相同
				//就说明多了一些最短路条数
                if(cost[j]<cost[k]+arr[j])   //援兵量能更新
                {
                    cost[j]=cost[k]+arr[j];
                    path[j]=k;

                }
            }

        }
    }

}
void print(int x)
{
    if(x==-1) return;
    print(path[x]);
    cout<<x<<" ";
}
int main()
{

    cin>>n>>m>>s>>d;
    memset(arr,0,sizeof(arr));
    memset(dismap,0x3f,sizeof(dismap));
    for (int j = 0; j <n ; ++j) {
        cin>>arr[j];
    }
    for (int i = 0; i <m ; ++i) {
        int x,y,z;
        cin>>x>>y>>z;
        //此题是无向图
        dismap[x][y]=z;
        dismap[y][x]=z;
    }
    dijk(s);
    cout<<num[d]<<" "<<cost[d]<<endl;//打印最短路径条数和最大援兵数
    print(path[d]);
    cout<<d<<endl;
    return 0;
}

相关题目链接：

[P1364 医院设置 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)]: “ 样题一：P1364 医院设置”

题目详情 - L2-001 紧急救援 (25 分) (pintia.cn) ：样题三：L2-001 紧急救援 (25 分)

L2-001 紧急救援 (25 分)&&dijkstra - 灰信网（软件开发博客聚合） (freesion.com)：样题三参考资料