并查集

并查集（Disjoint Set）是一种非常精巧而实用的数据结构。用于处理不相交集合的合并问题。

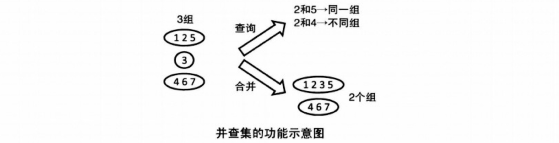
并查集用来管理元素分组情况。并查集可以高效地进行如下操作。

1.查询元素 a和元素 b是否属于同一组。
2.合并元素 a和元素 b所在的组。

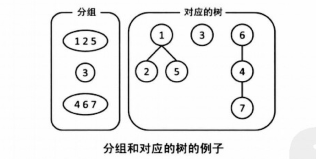
1.初始化

我们准备 n个节点来表示 n个元素。最开始时没有边。

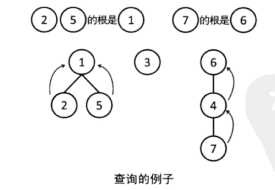
2.查询

为了查询两个节点是否属于同一组，我们需要沿着树向上走，来查询包含这个元素的树的根是谁。如果两个节点走到了同一个根，那么就可以知道它们属于同一组。

在下图中，元素 2 和元素 5都走到了元素 1，因此它们属于同一组。另一方面，由于元素 7 走到的是元素 6，因此同元素 2或元素 5 属于不同组。

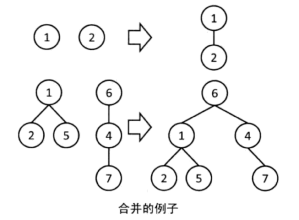
3.合并

像下图一样，从一个组的根向另一个组的根连边，这样两棵树就变成了一棵树，也就把两个组合并为一个组了。

4.路径压缩

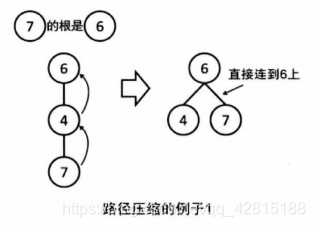
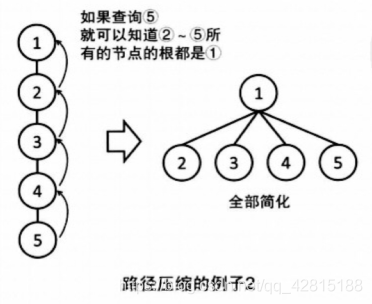
上面的查询程序 find() 沿着搜索路径找到根结点，这条路径可能很长。

优化：沿路径返回时，顺便把 i 所属的集改成根结点。下次再搜，复杂度是 O(1)。

这种方法称为路径压缩，在递归过程中，整个搜索路径上的元素所属的集都被改为根结点。

路径压缩的思想是，我们只关心每个结点的父结点，而并不太关心树的真正的结构。路径压缩不仅优化了下次查询，而且也优化了合并，因为合并时也用到了查询。

5.按秩合并

合并元素 x 和 y 时，先搜到它们的根结点；
合并这两个根结点：把一个根结点的集改成另一个根结点。
这两个根结点的高度不同，把高度较小的集合并到较大的集上，能减少树的高度。

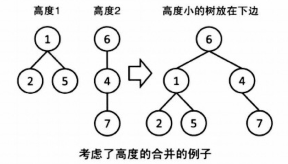
这样，在初始化时就要用一个数组定义元素 i的高度，在合并时更改。

下面代码加入了上述两个优化，我们用编号代表每个元素。数组 par[ ]表示的是父亲的编号，par[ x ] = = x 时，x 是所在的树的根。

int par[N];   //父亲
int rank[N];  //树的高度

// 初始化n个元素
void init(int n)
{
	for(int i = 0; i < n; i++)
	{
		par[i] = i;
		rank[i] = 0;
	}
}

// 查询树的根（路径压缩）
int find(int x)
{
	if(par[x] == x)
		return x;
	else
		return par[x] = find(par[x]);
}

// 合并x和y所属的集合（按秩合并）
void unite(int x, int y)
{
	x = find(x);
	y = find(y);
	if(x == y)  return;
	
	if(rank[x] < rank[y])
		par[x] = y;
	else
	{
		par[y] = x;
		if(rank[x] == rank[y])	rank[x]++;
	}
}

样题一：L2-024 部落 (25 分)

题目描述：

在一个社区里，每个人都有自己的小圈子，还可能同时属于很多不同的朋友圈。我们认为朋友的朋友都算在一个部落里，于是要请你统计一下，在一个给定社区中，到底有多少个互不相交的部落？并且检查任意两个人是否属于同一个部落。

输入格式：

输入在第一行给出一个正整数N（≤104），是已知小圈子的个数。随后N行，每行按下列格式给出一个小圈子里的人：

K P[1] P[2] ⋯ P[K]

其中K是小圈子里的人数，P[i]（i=1,⋯,K）是小圈子里每个人的编号。这里所有人的编号从1开始连续编号，最大编号不会超过104。

之后一行给出一个非负整数Q（≤104），是查询次数。随后Q行，每行给出一对被查询的人的编号。

输出格式：

首先在一行中输出这个社区的总人数、以及互不相交的部落的个数。随后对每一次查询，如果他们属于同一个部落，则在一行中输出Y，否则输出N。

输入样例：

输出样例：

1
2
3

10 2
Y
N结尾无空行

#include <bits/stdc++.h>
using namespace std;
const int  N=10005;
int par[N];       //父亲
int deep[N];      //树的高度
int isroot[N];    //用来记录互不相交的部落的个数。如果同属于一个部落，那个这个部落的元素的根节点都是一样的。
                  //所以只要统计有多少个根节点就可以知道有多少个互不相交的部落个数
set<int> st;      //集合能很好的过滤到重复元素，可以很方便的用来统计不是重复元素的个数
void init(int n)
{
    for(int i=0;i<n;i++)
    {
        par[i] = i;
        deep[i] =0;
    }
}
int find(int x)
{
    if(par[x] == x ) return x;
    else return par[x] = find(par[x]);
}
void unite(int x,int y)
{
    x=find(x);
    y=find(y);
    if(x==y) return;
    if(deep[x]<deep[y])
    {
        par[x]=y;
    }else{
        par[y]=x;
        if(deep[x]==deep[y]) deep[x]++;
    }
}
int main() {
    int n;
    cin>>n;
    init(10005);
    memset(isroot,0,sizeof(isroot));
    int ans=0;
    for (int i = 0; i <n ; ++i) {
        int num,first;
        cin>>num>>first;
        st.insert(first);
        for (int j = 1; j <num ; ++j) {
            int next;
            cin>>next;
            st.insert(next);
            unite(first,next);
        }
    }
    //寻找互不相交的部落
    for (int l = 1; l <=st.size() ; ++l) {
        isroot[find(l)]=1;
    }
    for (int m = 1; m <=st.size() ; ++m) {
        ans+=isroot[m];
    }
    cout<<st.size()<<" "<<ans<<endl;
    int time;
    cin>>time;
    for (int k = 0; k <time ; ++k) {
        int a,b;
        cin>>a>>b;
        if(find(a)==find(b))
        {
            cout<<"Y"<<endl;
        }
        else{
            cout<<"N"<<endl;
        }
    }
    return 0;
}