OpenMP梯度积分法

OpenMP梯度积分法

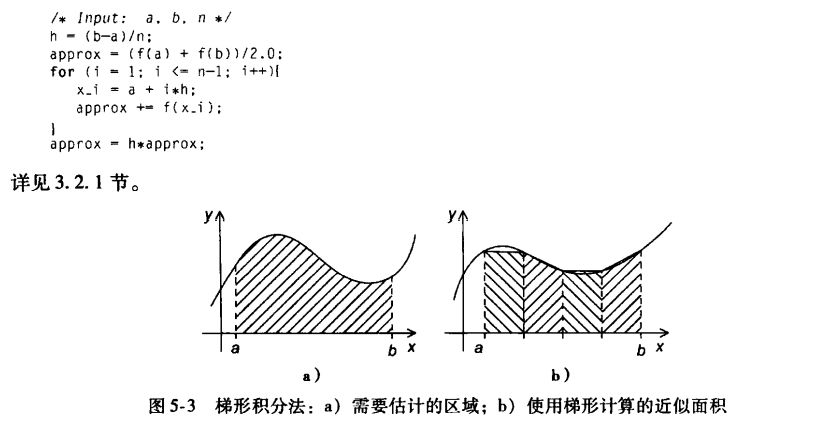
1.梯度积分法

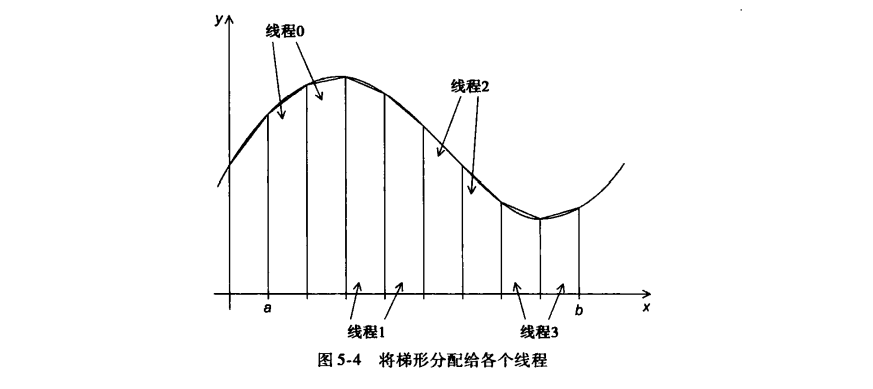
2.识别两类任务

1. 单个梯形的面积计算
2. 梯形面积求和

在2.1的任务中，没有任务间的通信，但这一组任务中的每一组任务都与2.2的任务通信

3.累加线程结果

​ 使用一个共享变量作为所有线程的和 ，每个线程可以将它计算的部分结果累加到共享变量中，让每个线程执行类似下面的语句：

#pragma omp critical
global_result += myresult;                //需要互斥访问

竞争条件，使用临界区解决。保证每次只有一个线程执行这段结构性代码。

4.程序完整代码

#include <stdio.h>
#include <stdlib.h>
#include <omp.h>

void Trap(double a,double b,int n,double *global_result_p);
int main(int argc, char *argv[]){
	double global_result = 0.0;
	double a,b;												//为了区分local_a,local_b
	int n;
	int thread_count;
	
	thread_count = 8;                                      	//指定你的线程数
	printf("Enter a,b, and n\n");
	scanf("%lf %lf %d",&a,&b,&n);
    
    //并行区开始
	#pragma omp parallel num_threads(thread_count)			//指定Trap函数由thread_count个线程执行
	Trap(a,b,n,&global_result);
	//并行区结束
    
	printf("With n = %d trapezoids, our estimate\n",n);
	printf("of the integral from %f to %f = %.4lf\n",a,b,global_result);
	
	return 0;
}
void Trap(double a,double b,int n,double *global_result_p)
{
	double h,x,my_result;
	double local_a,local_b;
	int i,local_n;											//local_n代表本进程被分配了多少个任务
	int my_rank = omp_get_thread_num();
	int thread_count = omp_get_num_threads();
	
	h = (b-a)/n;											//梯形底的长度
	local_n = n/thread_count;								//每个线程分配的梯形数，保证能整除
	local_a = a + my_rank*local_n*h;						//区间的左端点
	local_b = local_a + local_n*h;							//区间的右端点
	//对global_result共享部分和
    my_result = (f(local_a) + f(local_b))/2.0;				//f(x)是目标函数
	for(i = 1 ; i<=local_n-1; i++){
		x = local_a + i*h;
		my_result += f(x);
	}
	my_result = my_result*h;
    //
	#pragma omp critical									//临界区，这里可以直接使用OpenMP提供的reduction
	*global_result_p += my_result;							//线程将部分和结果累加到共享变量
}

5.总结

1. 核心是拆分任务区域，把子任务分配到个个线程
2. 共享变量的选取决定了可并行度
3. 通过共享变量实现了归约的操作(这里使用到了临界区)

6.参考资料

并行程序导论 （美）Peter S.Pacheco