BLISlab tutoril阅读

参考资料：

Git地址：https://github.com/flame/blislab 【代码包包含tutoril.pdf】

BLISlab: A Sandbox for Optimizing GEMM

Abstract

矩阵-矩阵乘法是科学计算中非常重要的基本运算，机器学习也越来越重要。这是一个非常简单的概念，可以在典型的高中代数课程中引入，但在实践中又非常重要，它在计算机上的实现仍然是一个活跃的研究主题。本笔记描述了一组使用该操作的练习，如何在具有分层内存(多个缓存)的现代cpu上获得高性能。它是基于blas类库实例化软件(BLIS)框架下的见解，通过公开一个模仿BLIS实现的简化“沙盒”来实现的。因此，它也成为BLIS优化的“众包”工具。

1.Introduction

矩阵-矩阵乘法(Gemm)经常被用作一个简单的例子，以提高如何在现代处理器上优化代码的意识。原因是该操作描述简单，很难完全优化，而且具有实际意义。在本文档中，我们将带领读者了解目前CPU架构中最快实现的技术。

1.1 Basic Linear Algebra Subprograms (BLAS)

基本线性代数子程序(BLAS)[10,5,4,14]为一组线性代数操作形成了一个接口，在此基础上构建了更高级别的线性代数库，如LAPACK[2]和libflame[19]。其思想是，如果有人针对给定的体系结构优化BLAS，那么所有以调用BLAS的方式编写的应用程序和库都将受益于这种优化。

BLAS被分为三组:一级BLAS(矢量-矢量操作)、二级BLAS(矩阵-矢量操作)和三级BLAS(矩阵-矩阵操作)。最后一组得益于这样一个事实:如果所有矩阵操作数的大小都是n × n，则O(n3)浮点运算对O(n)个数据执行，因此在内存层(主存、缓存和寄存器)之间移动数据的成本可以在很多次计算中平摊。因此，如果仔细执行这些操作，原则上可以实现高性能。

1.2 Matrix-matrix multiplication

特别地，BLAS通过(Fortran)调用支持具有双精度浮点数的Gemm:

1	`dgemm( transa, transb, m, n, k alpha, A,lda, B, ldb, beta, C, ldc)`

通过适当地选择转置a和转置b来计算:

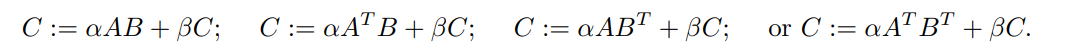
这里C是m × n, k是“第三维”。参数dla, dlb和dlc将在本文档后面进行解释。

在我们的练习中，我们考虑Gemm的简化版本:

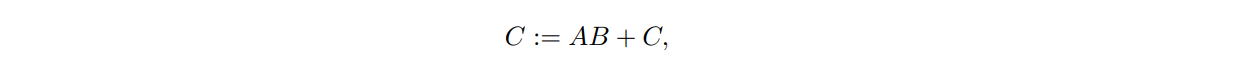
其中C是m × n, A是m × k, B是k × n。如果了解如何优化dgemm的这种特殊情况，那么可以很容易地将此知识扩展到所有3级BLAS功能。

1.3 High-performance implementation

高性能实现的复杂性使得BLAS(尤其是Gemm)的实现通常都是由默默无闻的专家来完成的，这些专家为硬件供应商开发数字库，例如IBM的ESSL、Intel的MKL、Cray的LibSci和AMD的ACML库。这些库通常是用汇编代码编写的(至少是部分)，并且针对特定的处理器高度专门化。

一篇关键论文[1]展示了“算法和体系结构”方法如何携手设计ar体系结构、编译器和算法，使BLAS能够用高级语言(Fortan)为IBM Power体系结构编写，并解释了在这些处理器上实现高性能的复杂性。便携式高性能ANSI C (PHiPAC)[3]项目随后提供了用C编写高性能代码的指南，并建议如何自动生成和优化以这种方式编写的Gemm。Au tomatatically tuning Linear Algebra Software (ATLAS)[17,18]建立在这些见解的基础上，使BLAS库的自动调优和自动生成成为主流。

在本文档的一部分中，我们讨论了有关该主题的最新论文，包括引入了实施Gemm[6]的Goto方法和该方法[16]的BLIS重构的论文，以及其他更直接相关的论文。

1.4 Other similar exercises

还有一些人基于Gemm组合了练习。与本文相关的最新成果有:乌尔姆大学Michael Lehn所作的“优化微内核:从纯C到SSE”，以及我们自己整理的关于“优化微内核”的维基。

1.5 We need you!

本文的目的是指导您实现Gemm的高性能实现。我们的别有用心是，用于实现BLAS的BLIS框架需要针对各种cpu高度优化的所谓微内核。在教你基本技巧的过程中，我们希望找到“那个人”将贡献最好的微内核。就把它当做我们版的高性能计算机达人秀吧。虽然我们在描述中关注的是Intel Haswell架构的优化，但是设置可以很容易地修改，从而帮助您(和我们)优化其他cpu。事实上，BLIS本身支持的体系结构包括AMD和Intel的x86处理器，IBM的Power处理器，ARM处理器和德州仪器的DSP处理器[15,12,8]。

2 Step 1: The Basics

2.1 Simple matrix-matrix multiplication

在我们的讨论中，我们将考虑计算：

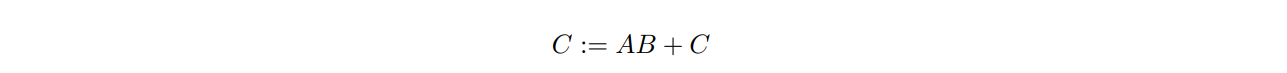
其中，A、B、C分别为m × k、k × n、m × n矩阵。

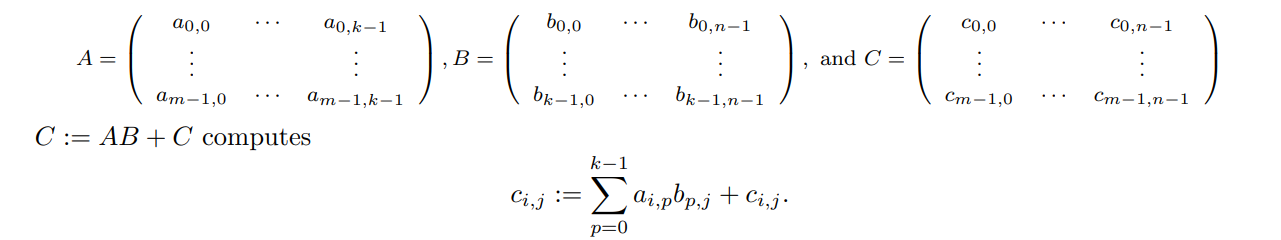
如果A、B和C存储在二维数组A、B和C中，下面的伪代码计算C:=
AB + C:

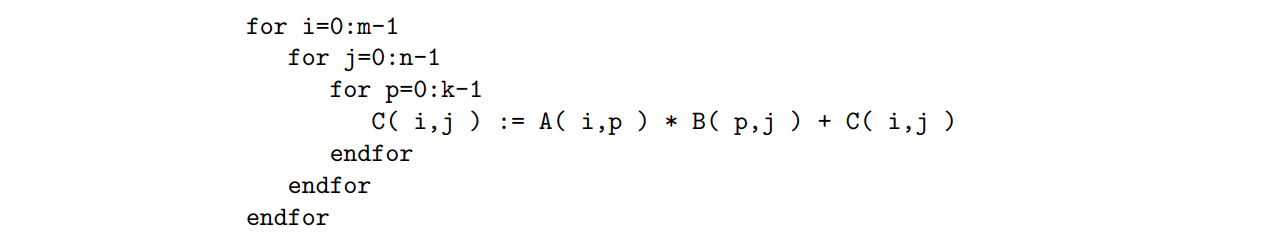
分别计算乘法和加法，计算需要2mnk个浮点运算(flop)。

2.2 Setup

为了让您高效地学习如何高效地进行计算，您可以在启动项目时准备好大部分基础设施。我们已经构造了子目录step1，有点像实现真正库might的项目。对于我们的目的来说，这可能是多余的，但是如何构建软件项目是一项值得学习的有用技能。

考虑图4，它演示了子目录step1的目录结构:

README是一个描述目录内容以及如何编译和执行代码的文件。

source .sh配置环境变量的文件。在那个文件中

BLISLAB USE INTEL设置是否使用INTEL编译器(true)或GNU编译器(false)。

BLISLAB USE BLAS指示您的参考dgemm是否使用外部BLAS库实现(如果您的机器上安装了这样的BLAS库，则为true)，还是简单的三重循环实现(false)。

COMPILER OPT LEVEL设置GNU或Intel编译器的优化级别(O0, O1, O2, O3)。
(请注意，例如，O3由大写字母“O”和数字“3”组成。)

OMP NUM THREADS and BLISLAB IC NT设置用于并行版本的线程数
代码。对于第1步，将它们都设置为1。

dgemm是实现dgemm的例程存在的子目录。在其中

bl_dgemm_ref.c包含例程dgemm ref，它是dgemm的一个简单实现，如果BLISLAB_use_BLAS = false，您将使用它来检查实现的正确性。

my_dgemm.c包含例程dgemm，它最初是dgemm的一个简单实现，您将优化它作为掌握如何优化gemm的第一步的一部分。

Bl_dgemm_util.c包含稍后会派上用场的实用程序例程

include这个目录包含包含各种宏定义和其他头信息的文件。

lib此目录将保存由您实现的源文件(libblislab. lib)生成的库。libblislab.a)您还可以在此目录中安装参考库(例如OpenBLAS)以比较性能。

test 这个目录包含“测试驱动程序”和各种实现的正确性/性能检查脚本。

test_bl_demm .c包含测试例程bl_demm的“测试驱动程序”。

test_bl_dgemm.x是test_bl_dgemm.c的可执行文件。

Run_bl_dgemm.sh包含一个bash脚本，用于收集性能结果。

tacc_run_bl_dgemm.sh contains a SLURM script for you to (optionally) submit the job to the Texas Advanced Computing Center (TACC) machines if you have an account there.

2.3 Getting started

我们希望您从my_dgemm.c中的实现开始，并通过应用各种标准优化技术对其进行优化。该文件中的初始实现是具有图2中给出的三个循环的简单实现。首先要注意的是二维数组如何以所谓的列-主序映射到内存。这种选择的原因是最初的BLAS假定数组的列主存储，因为该接口首先是为Fortran用户提供的。检查

我们注意到，每个操作数都是一个宏。考虑文件的早期

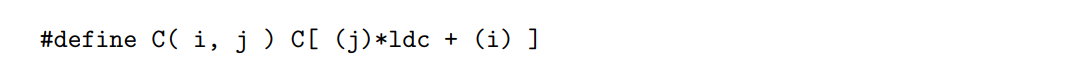
地址C处的线性数组用于存储元素Ci,j，因此i,j元素被映射到位置j * ldc + i。查看它的方法是C的每一列都是连续存储的。但是，可以把矩阵C看作是嵌入在一个更大的数组中，该数组有ldc行，因此访问一行就意味着跨ldc遍历数组C。二维数组C的前维数通常是指这个较大数组的行维数，因此变量ldc (C的前维数)。下图说明了这三个矩阵:

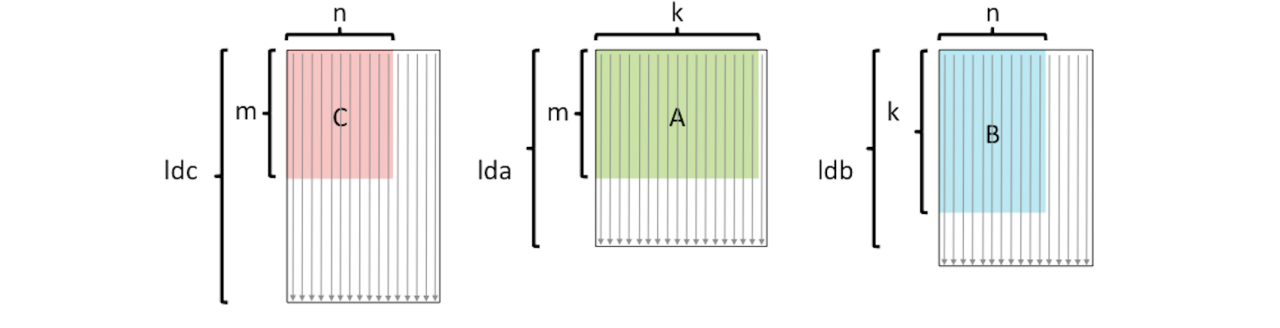
其中箭头表示列是连续存储的。

2.3.1 Configure the default implementation

默认情况下，练习编译并链接到Intel的icc编译器，该编译器将对代码应用编译器优化(O3级)。您需要通过以下命令设置环境变量:

1	`source sourceme.sh`

在终端中，您将看到输出:

1 2	`BLISLAB_USE_INTEL = TRUE COMPILER_OPT_LEVEL = O3`

2.3.2 Compile, execute and collect results

如果您无法访问Intel的编译器(icc)，请阅读第2.3.2小节和2.3.3小节，并继续阅读第2.3.5小节。

您可以编译、执行代码并通过执行收集性能结果

make clean
make
cd test
./run_bl_dgemm.sh

在子目录step1中。您将看到性能结果输出:

您可以在run_bl_dgemm.sh中更改采样块大小。请注意，如果代码中有错误，这些错误将被报告为，例如，

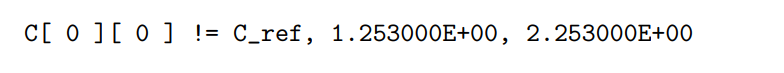
2.3.3 Draw the performance graph

最后，您可以使用MATLAB用我们的脚本绘制性能图。在test子目录下，执行后

1	`./collect_result_step1`

你会得到一个MATLAB文件“step1_result.m”，具有性能结果。然后你可以执行

1	`bl_dgemm_plot.m`

在MATLAB中，然后生成性能图。

2.3.4 Change to the GNU compiler

由于我们希望您明确地了解什么样的技巧可以带来高性能，并且由于有些人可能无法访问Intel编译器，因此接下来应该改为使用GNU C编译器。为此，你必须编辑sourceme.sh:

1	`BLISLAB_USE_INTEL=false`

然后，类似于默认设置，您需要通过执行以下命令来设置环境变量:

1	`source sourceme.sh`

在终端，你会观察到:

1 2	`BLISLAB_USE_INTEL = false COMILER_OPT_LEVEL = O3`

2.3.5 Turn off optimization

接下来，我们希望您关闭编译器执行的优化。这有三个目的:首先，这意味着您将必须显式地执行优化，这将允许您了解架构和算法如何交互。其次，优化编译器很可能会试图“撤销”您显式试图完成的任务。第三，在代码中构建的技巧越多，编译器就越难找出优化的方法。

你需要先编辑sourceme.sh:

1	`COMILER_OPT_LEVEL = O0`

然后，类似于默认设置，您需要通过执行以下命令来设置环境变量:

1	`source sourceme.sh`

在终端中，您将看到输出:

1 2	`BLISLAB_USE_INTEL = false COMILER_OPT_LEVEL =O0`

2.3.6 (Optional) Use optimized BLAS library as reference implementation

默认情况下，您的参考Gemm实现是一个非常缓慢的三循环实现。如果你在测试机器上安装了BLAS库，你可以通过设置该库中的dgemm作为你的参考实现:

1	`BLISLAB_USE_BLAS=true`

在sourceme.sh。如果使用Intel编译器，则不需要显式指定MKL的路径。但是，如果使用GNU编译器，则需要指定BLAS库的路径。例如，您可能希望从https://github.com/flame/blis安装我们的BLIS库到/home/lib/blis目录同时在sourceme .sh中设置

1	`BLAS_DIR=/home/lib/blis`

执行**$ source sourceme .sh**后，你会看到:

1 2	`BLISLAB_USE_BLAS = true BLAS_DIR = /home/lib/blis`

现在，您的实现的性能和准确性将与这个优化的库例程进行比较。

2.4 Basic techniques

在本小节中，我们将介绍一些基本的交易技巧。

2.4.1 Using pointers

既然优化被关闭了，那么矩阵元素所在地址的计算将显式地公开。(优化编译器可以消除这种开销。)您要做的是更改my_gemm.c中的实现，以便它使用指针。在这样做之前，您可能需要备份原始的my_gemm.c，以防需要从头开始重新启动。实际上，在每个步骤中，您可能都希望在单独的文件中备份前面的实现

这是基本的想法。假设我们想把C中的所有元素都设为0。一个基本的循环，按照在my_gemm.c中找到的内容来设计

for( i = 0; i < m; i++){
    for( j = 0; j < n; j++){
        C(i,j) =0.0;
    }
}

Using pointers, we might implement this as

double *cp;
for( j = 0; j < n; j++){
    cp = &C[ j*ldc ];			//point cp to top of ith column
    for( i = 0; i < m; i++){
        *cp++ = 0.0;		//set element that cp points to to zero and
    }		//advance the pointer
}

注意，我们有意地交换了循环的顺序，以便向前移动指针将我们带到C的列中。

2.4.2 Loop unrolling

每次通过内部循环更新循环索引i和指针cp都会产生相当大的开销。

因此，编译器将执行循环展开。使用展开因子4，我们将C设置为0的简单循环变成

double *cp;

for( j = 0; j < n; j++){
    cp = &C[ j * ldc ];
    for( i = 0; i < m; i+=4){
        *(cp+0) = 0.0;
        *(cp+1) = 0.0;
        *(cp+2) = 0.0;
        *(cp+3) = 0.0;
        cp+=4;
    }
}

重要的

i和cp现在每四次迭代才更新一次。
(cp+0)使用称为间接寻址的机器指令，这比使用(cp+k)计算更有效，其中k是变量。
当它从内存中输入数据到缓存中时，每次输入一条64字节的缓存线。这意味着以64字节的块访问连续数据可以减少内存层之间的内存移动成本。

请注意，在展开时，如果m不是4的倍数，则可能必须处理“边缘”。

为了这个练习，你不需要担心这个边缘，只要你明智地选择你的采样块大小，就像第2.5节重申的那样。

2.4.3 Register variables

注意，只有当数据存储在寄存器中时，计算才会发生。编译器将自动转换代码，以便插入将某些数据放入寄存器的中间步骤。可以给编译器一个提示，将某些数据保存在寄存器中是很好的，如下面的例子所示:

double *cp;

for( j = 0; j < n; j++){
    cp = &C[ j * ldc ];
    for( i = 0; i < m; i+=4){
        register double c0 =0.0,c1=0.0,c2=0.0,c3=0.0;
        *(cp+0) = c0;
        *(cp+1) = c1;
        *(cp+2) = c2;
        *(cp+3) = c3;
        cp+=4;
    }
}

2.5 A modest first goal

现在我们要求您使用上面讨论的技术来优化my_dgemm.c。现在，只需要考虑如何为较小的矩阵获得更好的性能。具体来说，请看下面这张图:

我们想让你做的是编写你的代码，使C的mR × nR块保存在寄存器中。你可以选择mR和nR，但是你需要用这些选项更新文件include/bl_config.h。这确保了测试驱动程序只尝试这些块大小的倍数的问题大小，所以您不必担心“边缘”。

您将注意到，即使对于可以放入某个缓存内存中的较小的矩阵，您的实现(比您可能已安装的MKL或其他优化的BLAS库的实现差得多)。原因是编译器没有为浮点运算使用最快的指令。可以通过使用向量intrinsic funtions函数(允许您从C显式地利用它们)或通过在汇编代码中编码来访问这些函数。现在，我们还没到那一步。我们将
在步骤3中讨论更多。

3 Step 2: Blocking

3.1 Poorman’s BLAS

本练习的第1步使您认识到，随着基于缓存的体系结构的出现，Gemm的高性能实现需要仔细注意数据在内存层之间移动的成本和对该数据的计算的摊薄。为了保持这种可管理性，认识到只有使用相对较小的矩阵执行矩阵-矩阵乘法的“内核”需要高度优化，这是有帮助的，因为使用较大的矩阵的计算可以被分块，然后使用这样的内核而不会对整体性能产生不利影响。这一见解在[9]中得到了明确的提倡。

这有时被称为“穷人的BLAS”，因为如果一个人只能负担得起优化矩阵-矩阵乘法(使用子矩阵)，那么就可以构建Gemm，以及其他重要的矩阵-矩阵运算，即三级BLAS。我们稍后将看到的是，从模块化和性能的角度来看，这实际上是一个好主意。

在上一节中，您已经看到了分块的示例。

3.2 Blocked matrix-matrix multiplication

分块Gemm以利用处理器的分层内存的关键是理解当这些矩阵被分块时如何计算C:= AB + C。分块

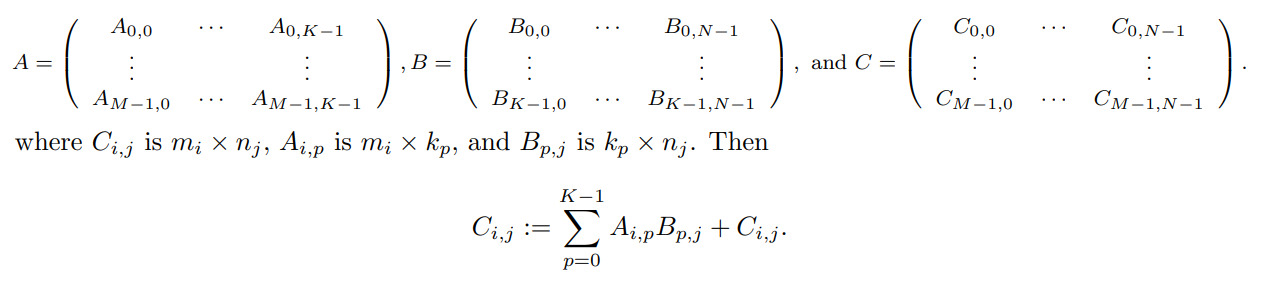
3.3 Your mission, if you choose to accept it

我们现在要求您在my_dgemm中实现分块矩阵-矩阵乘法。具体来说，对于小矩阵，您可以获得比大矩阵更好的性能，因为小矩阵适合缓存。将矩阵划分为能够获得更高性能的子矩阵，您将看到，即使对于更大的矩阵，所得到的实现也能保持更好的性能

4 Step 3: Blocking for Multiple Levels of Cache

4.1 The Goto Approach to Implementing gemm

2000年左右，Kazushige Goto用他的技术彻底改变了Gemm在当前cpu上的实现方式，该技术首次发表在论文[6]上。

最近在[16]中描述了这种方法的进一步“重构”。

BLIS框架的优点是它将必须高度优化的内核(可能使用向量intrinsic或在汇编代码中)减少为微内核。在本节中，我们将简要描述该方法的重点。然而，我们强烈建议读者熟悉以上两篇论文本身。

图3(左)说明了Goto方法为三层缓存(L1、L2和L3)构建分块的方式。在BLIS框架中，实现就是这样结构的，因此只有底层的微内核需要针对给定的体系结构进行高度优化和定制。在最初的GotoBLAS实现(现在维护为OpenBLAS[11])中，从围绕微内核的第二个循环开始的操作是定制的。为了获得最佳性能，所有数据都是连续访问的，这就是为什么在到达微内核之前的某个时刻，数据是按照箭头所示的顺序打包的:

现在，注意上图中A块的每一列都乘以B块对应行中的每个元素(我们称这些A块和B块为微面板)。这意味着L2缓存的延迟(从缓存中引入A微面板元素所需的时间)可以平摊到2nR flop上。

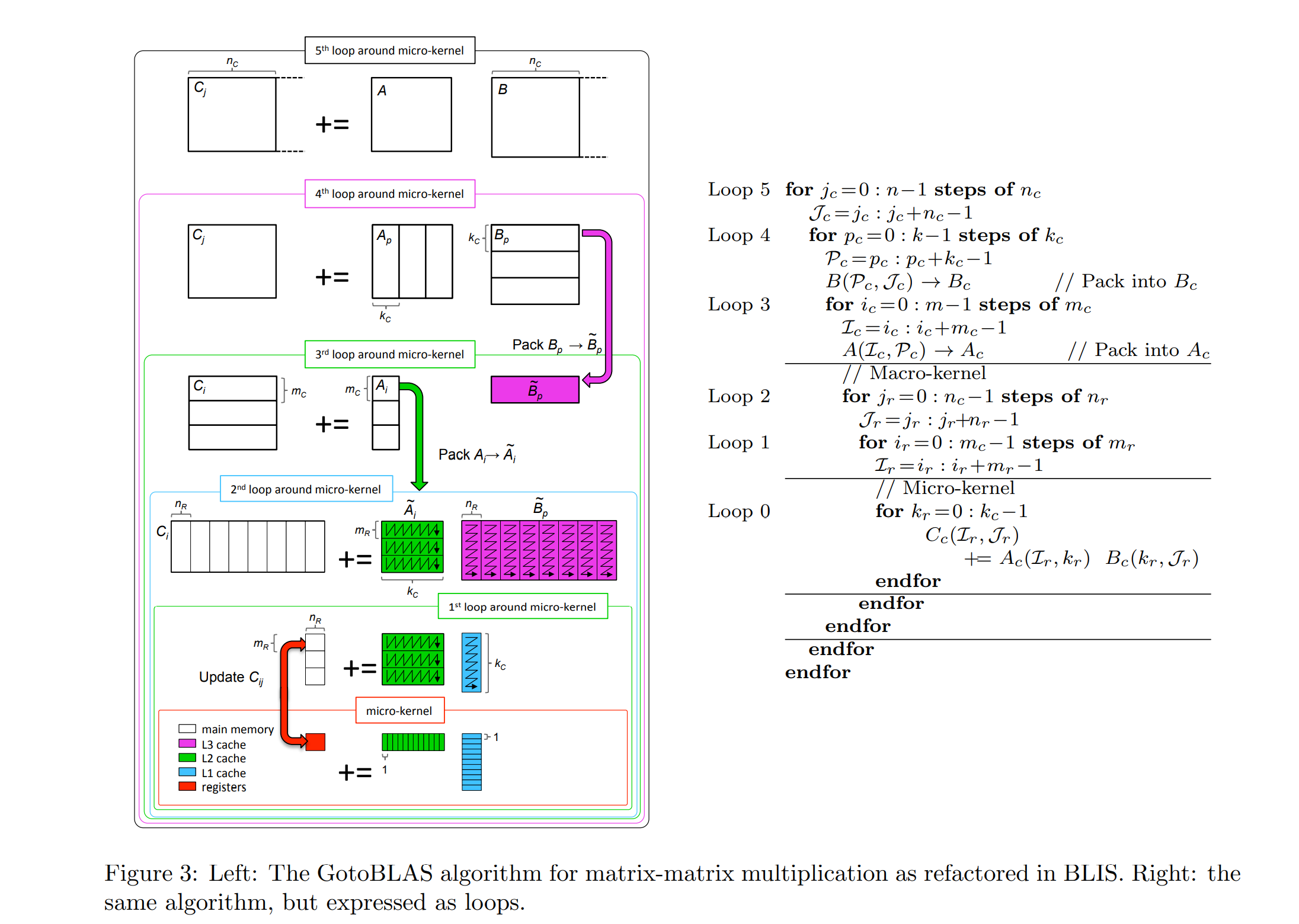
出于这个原因，我们可以组织计算，使A的微面板通常驻留在L2缓存中。实际上，我们可以做得更好:当A和B的微面板的一列发生排名1的更新时，A的微面板的下一列可以被带入寄存器，这样计算就可以掩盖数据移动的成本。事实上，我们希望将B的微面板保留在L1缓存中(因为它将被A的许多微面板重用)，这限制了分块参数kC。

有人可能会问，上述方案是否是最优方案。在[7]中给出了一个理论，表明在一个理想化的模型下，上述是局部最优的(在某种意义上，假设数据在层次结构中的某个内存层中，在该级别上提出的阻塞最优地与下一个内存层平摊数据移动的成本)。[13]给出了指导各种分块参数选择的理论。

4.2 Setup

图4说明了子目录step3的目录结构。与步骤1相比，我们对以下目录/文件进行了修改/添加:

kernels 这个目录包含各种架构的微内核实现

bd_gemm_ukr.c给出了一个原生的C实现

bl_dgemm_int_kernel.c gives an AVX/AVX2 intrinsics micro-kernel implementation for Haswell architecture.

bl_dgemm_asm_kernel.c gives an AVX/AVX2 assembly micro-kernel implementation for Haswell architecture.

4.3 Advanced techniques

You can find the vector instructions online:

Intel Intrinsics Guide

Intel ISA Extensions

4.3.1 An introduction example for “axpy”

我们提供了一个实现“axpy”的示例，以演示如何使用Intel AVX intrinsic和Assembly(在misc/examples子目录中)。

这个例子可以作为学习基本broacast/fma/load/store指令的一个很好的起点。此外，这个示例实际上是4×4 rank-1更新的“broadcast”实现的原语。

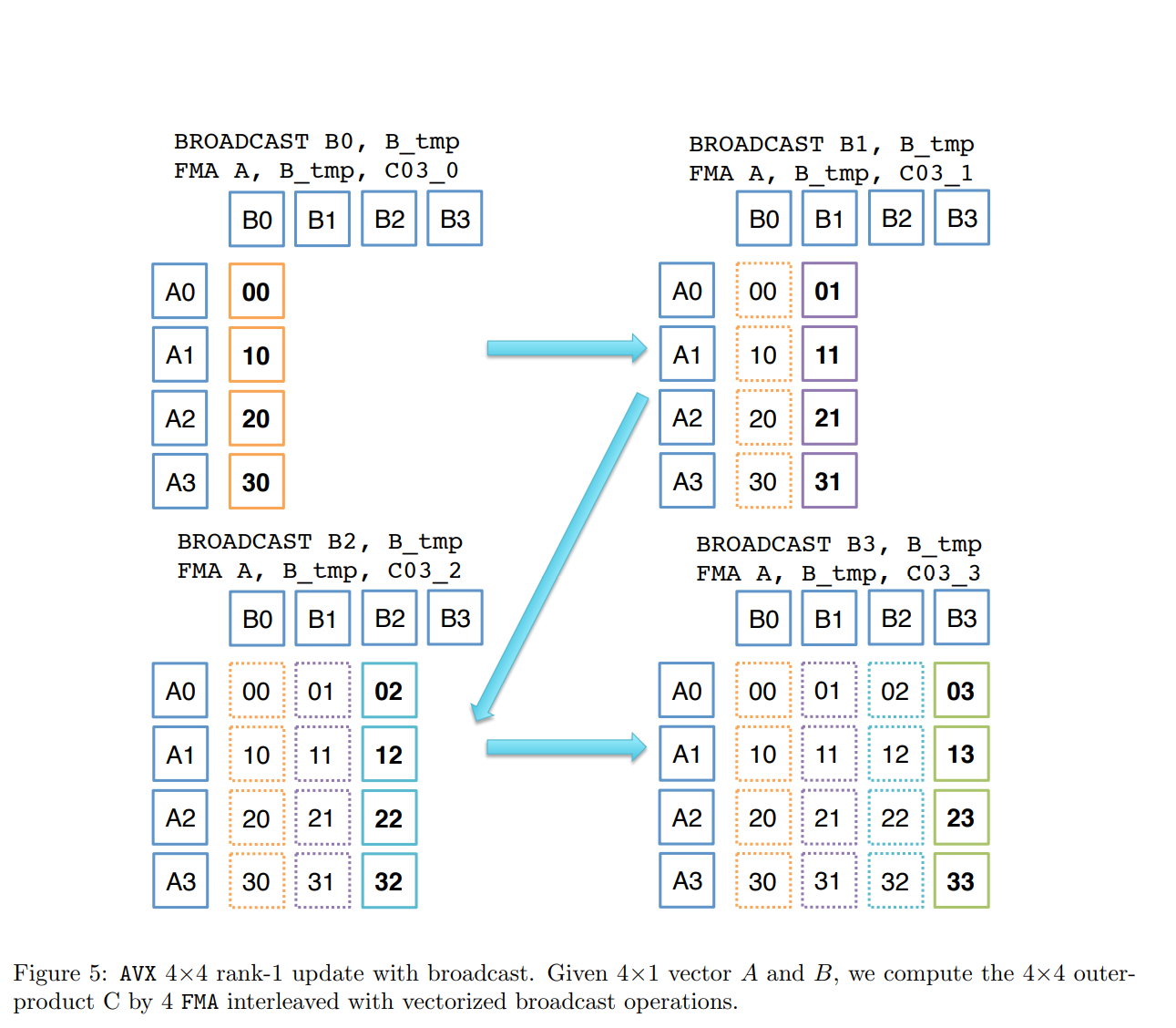
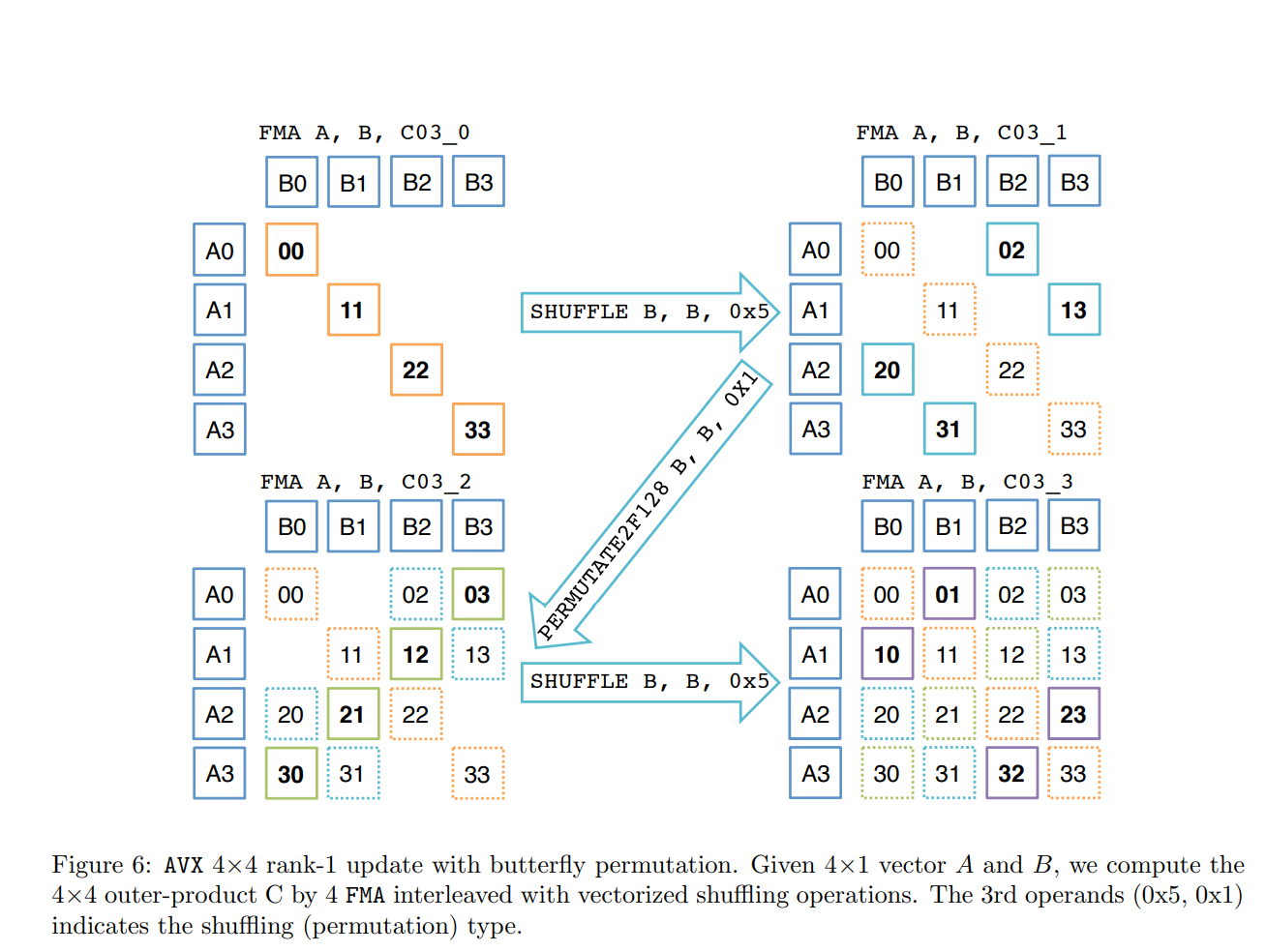
4.3.2 4×4 rank-1 update

微内核实现可以归结为4×4级别1的更新。有两种可能的实现:一种基于广播(图5)，另一种是蝴蝶排列(图6)。您还可以尝试其他可能的实现。

4.4 Your mission, if you choose to accept it

我们在my_dgemm中为您提供了简化BLIS框架的参考实现。代码的组织方式与图3所示相同。但是，每个循环中的步长并没有很好地选择，并且微内核实现是一个简单的C版本。因此。您不会期望代码具有高性能。我们要你做的就是:

在include/bl_config.h文件中指定分块参数mC, nC, kC和微内核大小参数mR, nR;
使用矢量intrinsic或汇编代码实现高效的微内核。将代码放在kernels/bl_dgemm_int_kernel.c(用于向量intrinsic)或kernels/bl_dgemm_asm_kernel.c(用于as汇编)中。需要在“include/ BL_config.h”中修改“BL_MICRO_KERNEL”，指定微内核的函数名。