矩阵乘法计算拆分展示

矩阵乘法计算拆分展示

通用矩阵乘概念

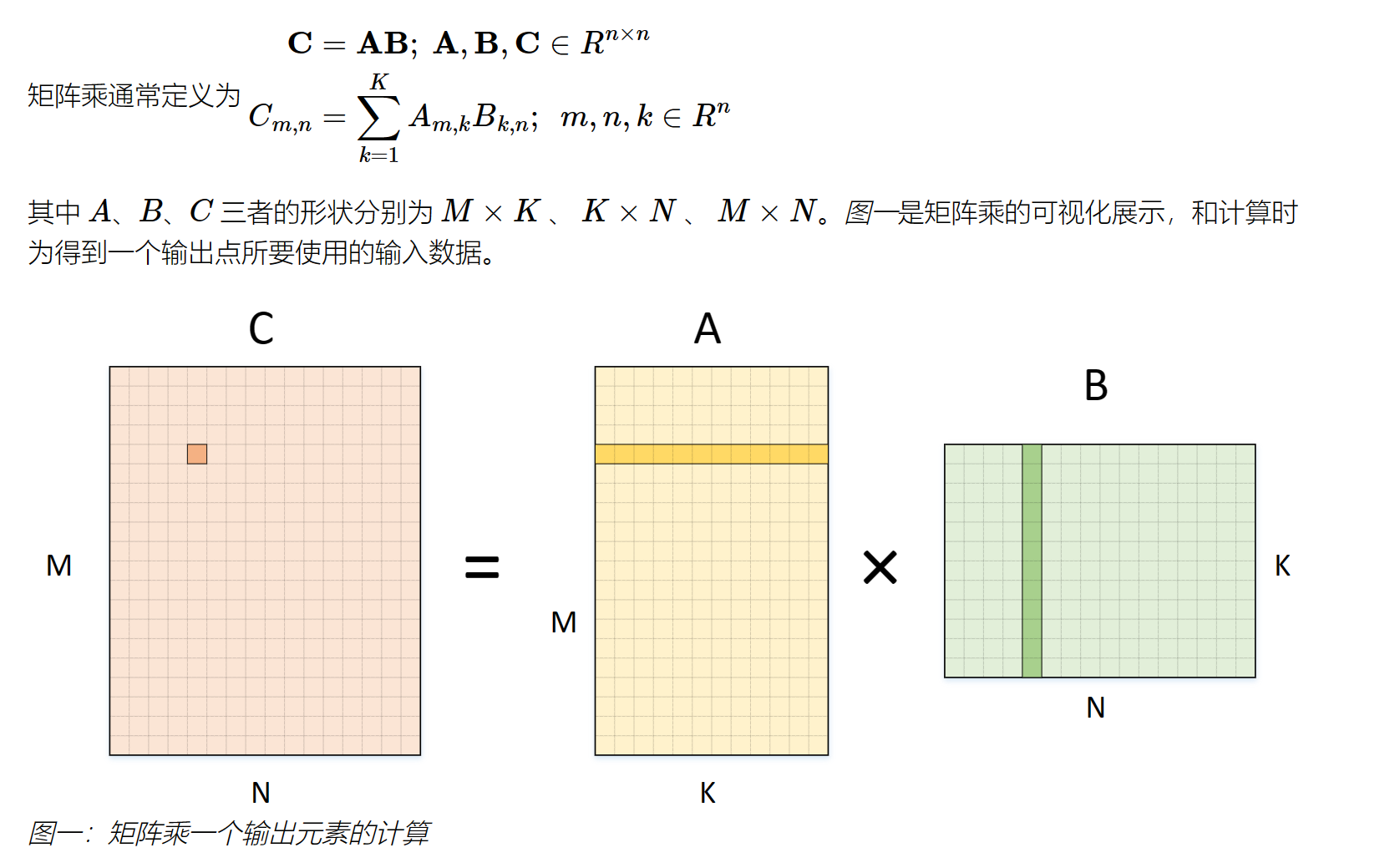
image-20230219171156738

1
2
3
4
5
6
7
8
9
for(int i = 0; i < m; i++){				//遍历C矩阵各行，其行数与A的行数相等 
    for(int j = 0; j < n; j++){			//遍历C矩阵i行j列
        c[i][j] = 0;
        for(int p = 0; p < k; p++){		//用p循环累加和计算C[i][j] 
            //计算区域
           C[i][j] += A[i][p] * B[p][j];		//遍历A矩阵各行与B矩阵各列
        }
    }
}

计算拆分展示

图四将输出计算拆分为 1 × 4 的小块，即将 N 维度拆分为两部分。计算该块输出时，需要使用 A 矩阵的1行，和 B 矩阵的4列 。

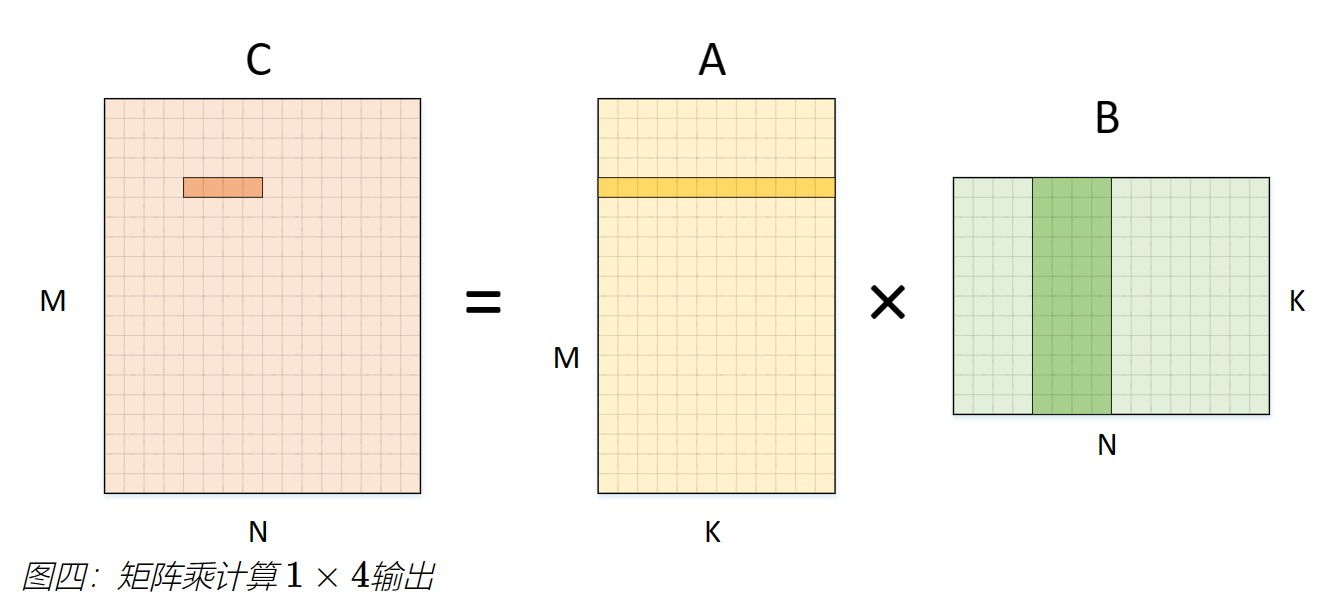
image-20230219171904249

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
for(int i = 0; i < m; i++){				//遍历C矩阵各行，其行数与A的行数相等 
    for(int j = 0; j < n; j +=4){			//遍历C矩阵j-j+3列
        c[i][j + 0] = 0;
        c[i][j + 1] = 0;
        c[i][j + 2] = 0;
        c[i][j + 3] = 0;
        for(int p = 0; p < k; p++){		//用p循环累加和计算C[i][j] 
            //计算区域
            //遍历A矩阵各行与B矩阵各列
           C[i][j + 0] += A[i][p] * B[p][j + 0];    
           C[i][j + 1] += A[i][p] * B[p][j + 1];
           C[i][j + 2] += A[i][p] * B[p][j + 2];
           C[i][j + 3] += A[i][p] * B[p][j + 3];
        }
    }
}

最内侧计算使用的矩阵A的元素是一致的。因此可以将**A[i][p]**读取到寄存器中，从而实现4次数据复用。例如：

1
register double temp = A[i][p];

一般将最内侧循环称作计算核(micro kernel)

类似地，我们可以继续拆分输出M维度，从而在内测循环中计算 4 × 4 输出，如图五。

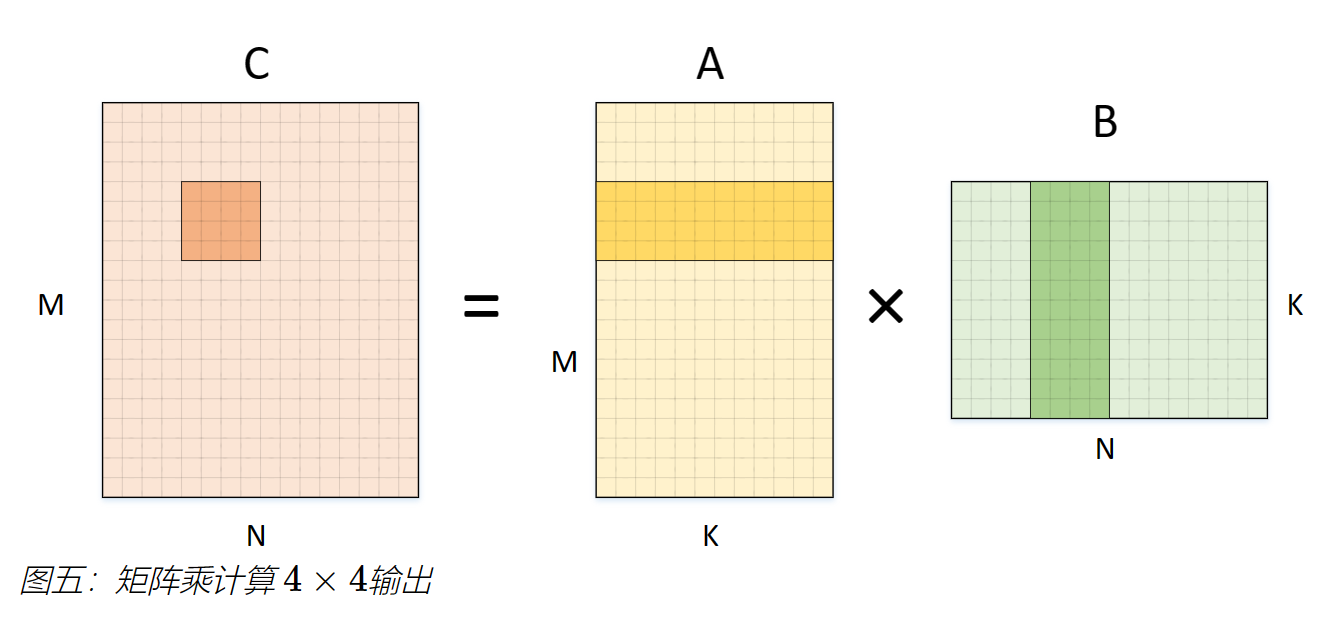
image-20230219174355047

同样的，将计算核心展开，可以得到下面的伪代码。这里我们将 1 × 4 中展示过的N维度的计算简化表示。这种拆分可看成是4 × 1 × 4，这样A和B的访存均可复用四次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
for(int i = 0; i < m; i+=4){				//遍历C矩阵i-i+3行，其行数与A的行数相等 
    for(int j = 0; j < n; j +=4){			//遍历C矩阵第j-j+3列
        c[i + 0][j + 0..3] = 0;
        c[i + 1][j + 0..3] = 0;
        c[i + 2][j + 0..3] = 0;
        c[i + 3][j + 0..3] = 0;
        for(int p = 0; p < k; p++){		//用p循环累加和计算C[i][j] 
            //计算区域
            //遍历A矩阵各行与B矩阵各列
           C[i + 0][j + 0..3] += A[i + 0][p] * B[p][j + 0..3];    
           C[i + 1][j + 0..3] += A[i + 1][p] * B[p][j + 0..3];
           C[i + 2][j + 0..3] += A[i + 2][p] * B[p][j + 0..3];
           C[i + 3][j + 0..3] += A[i + 3][p] * B[p][j + 0..3];
        }
    }
}

到目前为止。我们都是在输出的两个维度上展开，而整个计算还包含一个规约(Reduction)维度K。图六展示了在计算4 × 4输出时，将维度K拆分，从而每次最内侧循环计算出输出矩阵C的4/K的部分和。

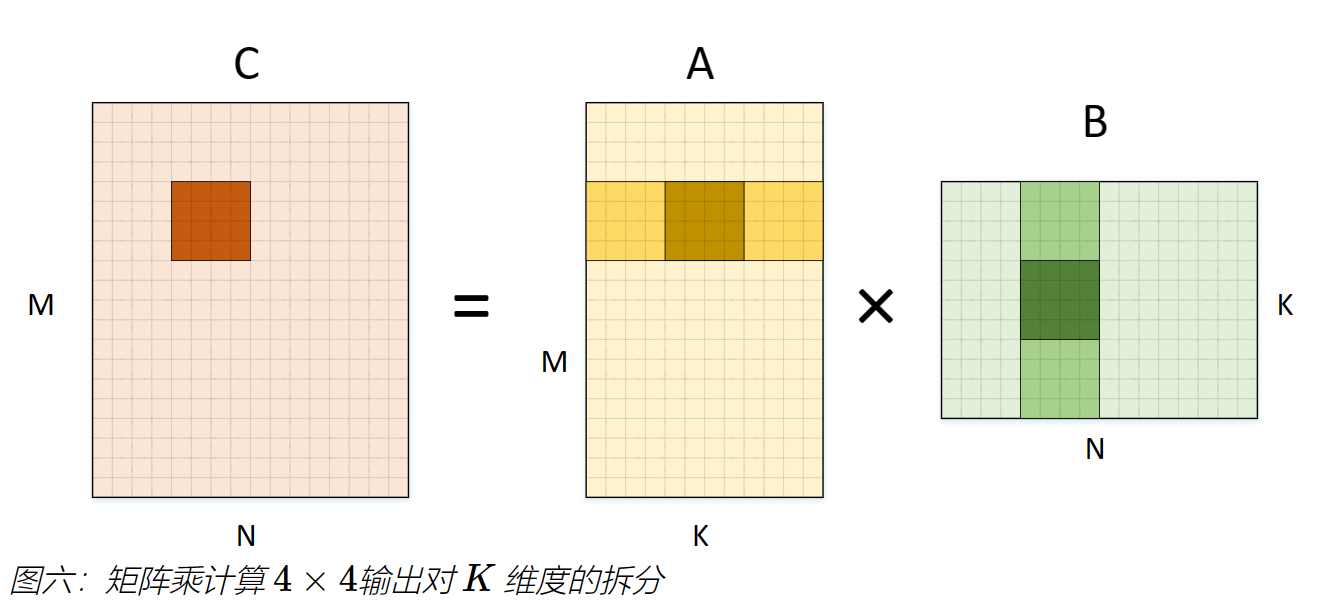
image-20230219180147184

下面展示的是这部分计算的展开伪代码，其中维度M和N已经被简写。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for(int i = 0; i < m; i+=4){				//遍历C矩阵i-i+3行，其行数与A的行数相等 
    for(int j = 0; j < n; j +=4){			//遍历C矩阵第j-j+3列
        c[i + 0..3][j + 0..3] = 0;
        c[i + 0..3][j + 0..3] = 0;
        c[i + 0..3][j + 0..3] = 0;
        c[i + 0..3][j + 0..3] = 0;
        for(int p = 0; p < k; p+=4){		//用p循环累加和计算C[i][j] 
            //计算区域
           C[i + 0..3][j + 0..3] += A[i + 0..3][p + 0] * B[p + 0][j + 0..3];    
           C[i + 0..3][j + 0..3] += A[i + 0..3][p + 1] * B[p + 1][j + 0..3];
           C[i + 0..3][j + 0..3] += A[i + 0..3][p + 2] * B[p + 2][j + 0..3];
           C[i + 0..3][j + 0..3] += A[i + 0..3][p + 3] * B[p + 3][j + 0..3];
        }
    }
}

在对M和N展开式，我们可以分别复用B和A的数据；在对K展开时，其局部使用的C的内存是一致的，那么K迭代时可以将部分和累加在寄存器中——最内层循环整个迭代一次写到C的内存中。

参考资料

通用矩阵乘（GEMM）优化算法 | 黎明灰烬 博客 (zhenhuaw.me)

HPC
Matrix GEMM

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！