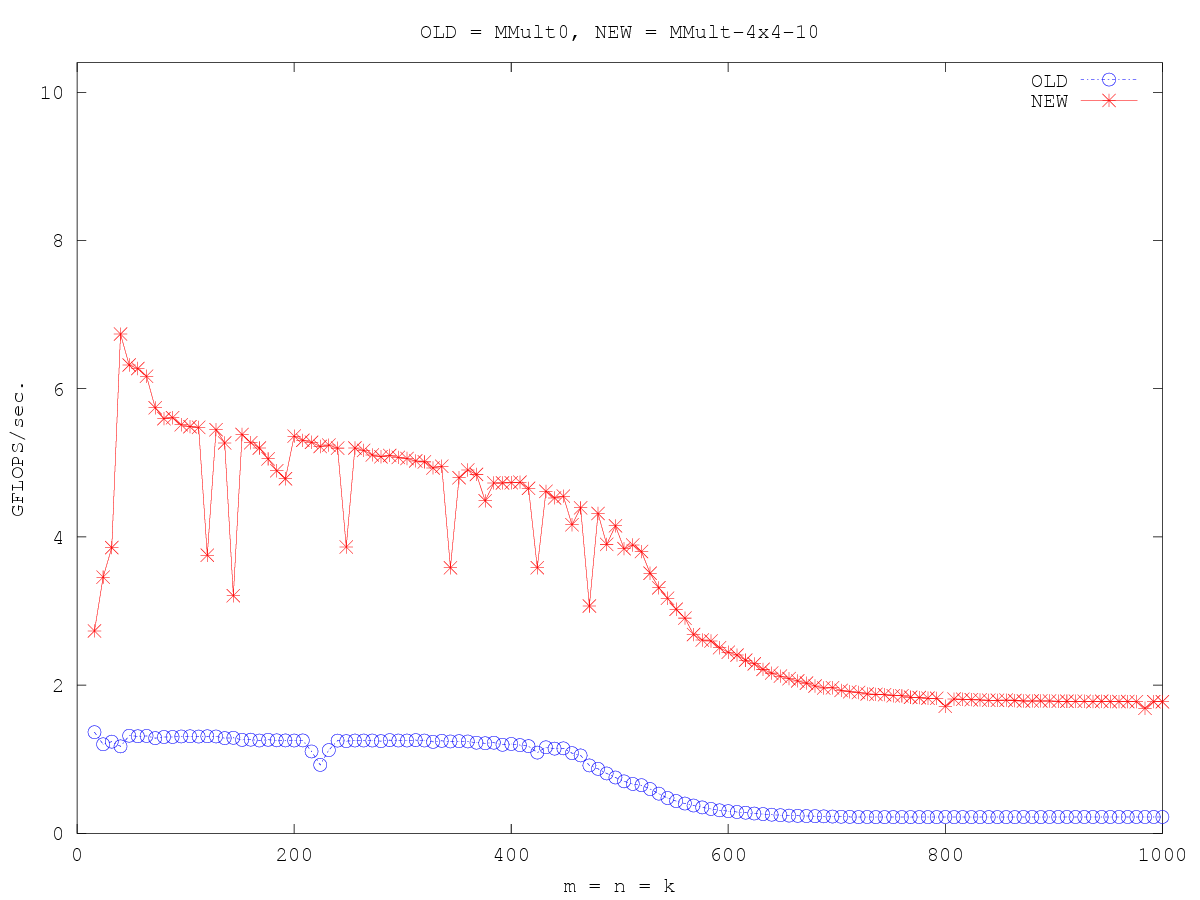
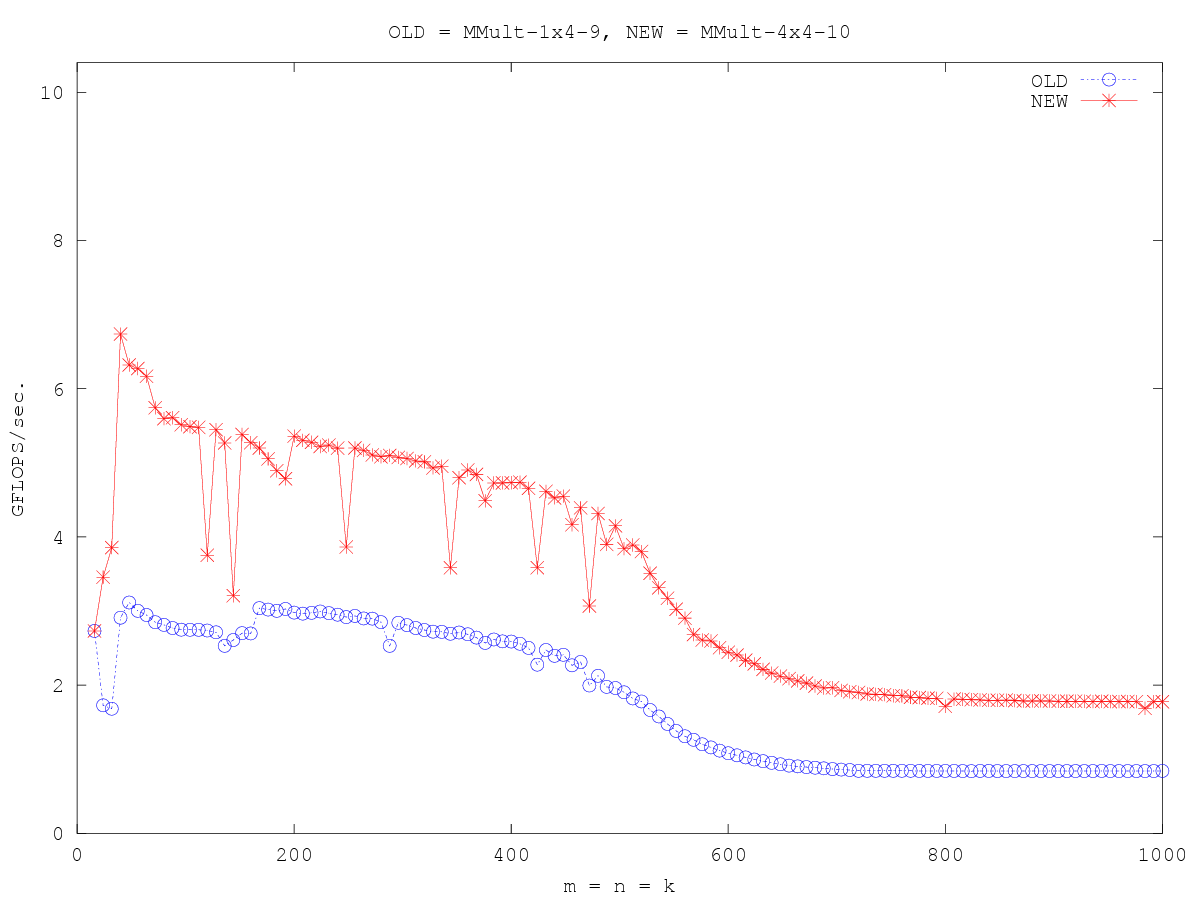
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
void AddDot4x4( int, double *, int, double *, int, double *, int );
void MY_MMult( int m, int n, int k, double *a, int lda,
double *b, int ldb,
double *c, int ldc )
{
int i, j;
for ( j=0; j<n; j+=4 ){
for ( i=0; i<m; i+=4 ){
AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
}
}
}
void AddDot4x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc )
{
int p;
register double
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
c_10_reg, c_11_reg, c_12_reg, c_13_reg,
c_20_reg, c_21_reg, c_22_reg, c_23_reg,
c_30_reg, c_31_reg, c_32_reg, c_33_reg,
a_0p_reg,
a_1p_reg,
a_2p_reg,
a_3p_reg,
b_p0_reg,
b_p1_reg,
b_p2_reg,
b_p3_reg;
double
*b_p0_pntr, *b_p1_pntr, *b_p2_pntr, *b_p3_pntr;
b_p0_pntr = &B( 0, 0 );
b_p1_pntr = &B( 0, 1 );
b_p2_pntr = &B( 0, 2 );
b_p3_pntr = &B( 0, 3 );
c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0;
c_10_reg = 0.0; c_11_reg = 0.0; c_12_reg = 0.0; c_13_reg = 0.0;
c_20_reg = 0.0; c_21_reg = 0.0; c_22_reg = 0.0; c_23_reg = 0.0;
c_30_reg = 0.0; c_31_reg = 0.0; c_32_reg = 0.0; c_33_reg = 0.0;
for ( p=0; p<k; p++ ){
a_0p_reg = A( 0, p );
a_1p_reg = A( 1, p );
a_2p_reg = A( 2, p );
a_3p_reg = A( 3, p );
b_p0_reg = *b_p0_pntr++;
b_p1_reg = *b_p1_pntr++;
b_p2_reg = *b_p2_pntr++;
b_p3_reg = *b_p3_pntr++;
c_00_reg += a_0p_reg * b_p0_reg;
c_01_reg += a_0p_reg * b_p1_reg;
c_02_reg += a_0p_reg * b_p2_reg;
c_03_reg += a_0p_reg * b_p3_reg;
c_10_reg += a_1p_reg * b_p0_reg;
c_11_reg += a_1p_reg * b_p1_reg;
c_12_reg += a_1p_reg * b_p2_reg;
c_13_reg += a_1p_reg * b_p3_reg;
c_20_reg += a_2p_reg * b_p0_reg;
c_21_reg += a_2p_reg * b_p1_reg;
c_22_reg += a_2p_reg * b_p2_reg;
c_23_reg += a_2p_reg * b_p3_reg;
c_30_reg += a_3p_reg * b_p0_reg;
c_31_reg += a_3p_reg * b_p1_reg;
c_32_reg += a_3p_reg * b_p2_reg;
c_33_reg += a_3p_reg * b_p3_reg;
}
C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg;
C( 1, 0 ) += c_10_reg; C( 1, 1 ) += c_11_reg; C( 1, 2 ) += c_12_reg; C( 1, 3 ) += c_13_reg;
C( 2, 0 ) += c_20_reg; C( 2, 1 ) += c_21_reg; C( 2, 2 ) += c_22_reg; C( 2, 3 ) += c_23_reg;
C( 3, 0 ) += c_30_reg; C( 3, 1 ) += c_31_reg; C( 3, 2 ) += c_32_reg; C( 3, 3 ) += c_33_reg;
}