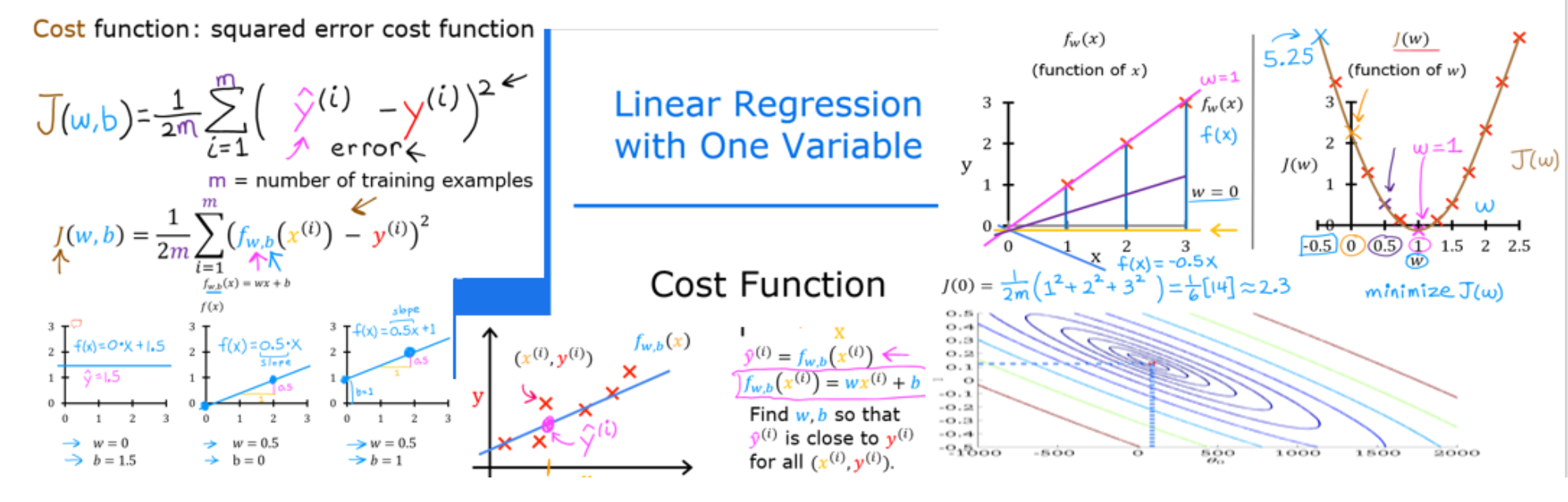
代价函数

代价函数

image-20230312164306128

目标

在本实验中，你将:

  • 你将实现和探索成本函数的线性回归伴随一个变量。

工具

在本实验室中，我们将使用:

  • NumPy，一个用于科学计算的流行库
  • Matplotlib，用于绘制数据的流行库
  • 本地目录的lab_utils_uni.py文件中的本地绘图例程
1
2
3
4
5
import nunpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_uni import plt_intuition, plt_stationary, plt_updata_onclick, soup_bowl
plt.style.use('./deeplearning.mplstyle')

问题意境

你想要一个模型，它可以根据房子的大小预测房价。让我们使用与上一个实验室之前相同的两个数据点——一个1000平方英尺的房子卖了30万美元，一个2000平方英尺的房子卖了50万美元。

Size(1000 sqft)Price(1000s of dollars)
1300
2500
1
2
x_train = np.array([1.0, 2.0])   #(size in 1000 square feet)
y_train = np.zrray([300.0, 500.0])	#(price in 1000s of dollars)

计算代价

这个作业中的术语“成本”可能会让人有点困惑，因为数据是住房成本。在这里，成本是衡量我们的模型预测房子目标价格的好坏。“价格”一词指的是住房数据。

含一个变量的成本方程为:

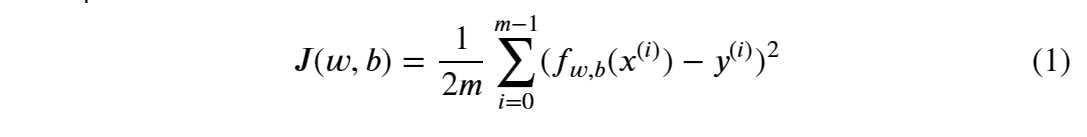
image-20230312165434160

在这里

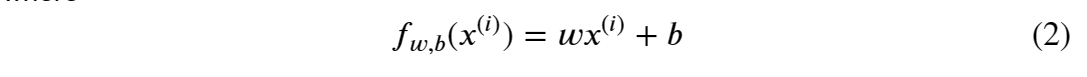
image-20230312165503613

  • f_w,b(x^i)是我们使用参数w,b来预测例子i。
  • （f_w,b(x^i) - y^i）^2 是目标值与预测值之间的差的平方
  • 这些差异被加在所有m例子上，再除以2m，得到代价函数 J（w,b）

注意，在讲座中，总和的范围通常是从1到m，而代码将从0到m-1。

下面的代码通过遍历每个示例来计算成本。在每个循环中:

  • f_wb，计算一个预测
  • 目标和预测之间的差值被计算和平方。
  • 这被加到总成本中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def compute_cost(x, y, w, b):
    """
    Computes the cost function for linear regression
    
    Args:
    	x (ndarray (m,)):Data, m examples
    	y (ndarray (m,)):target values
    	w,b (scalar)	:model parameters
    
    Returns
    	total_cost (float):The cost of using w,b as the parameters for linear regression to fit the data points in x and y
    """
    #number of training examples
    m = x.shape[0]
    
    cost_sum = 0
    for i in range(m):
        f_wb = w * x[i] + b
        cost = (f_wb - y[i])**2
        cost_sum = cost_sum + cost
    total_cost = (1/(2*m)) * cost_sum
    
    return total_cost

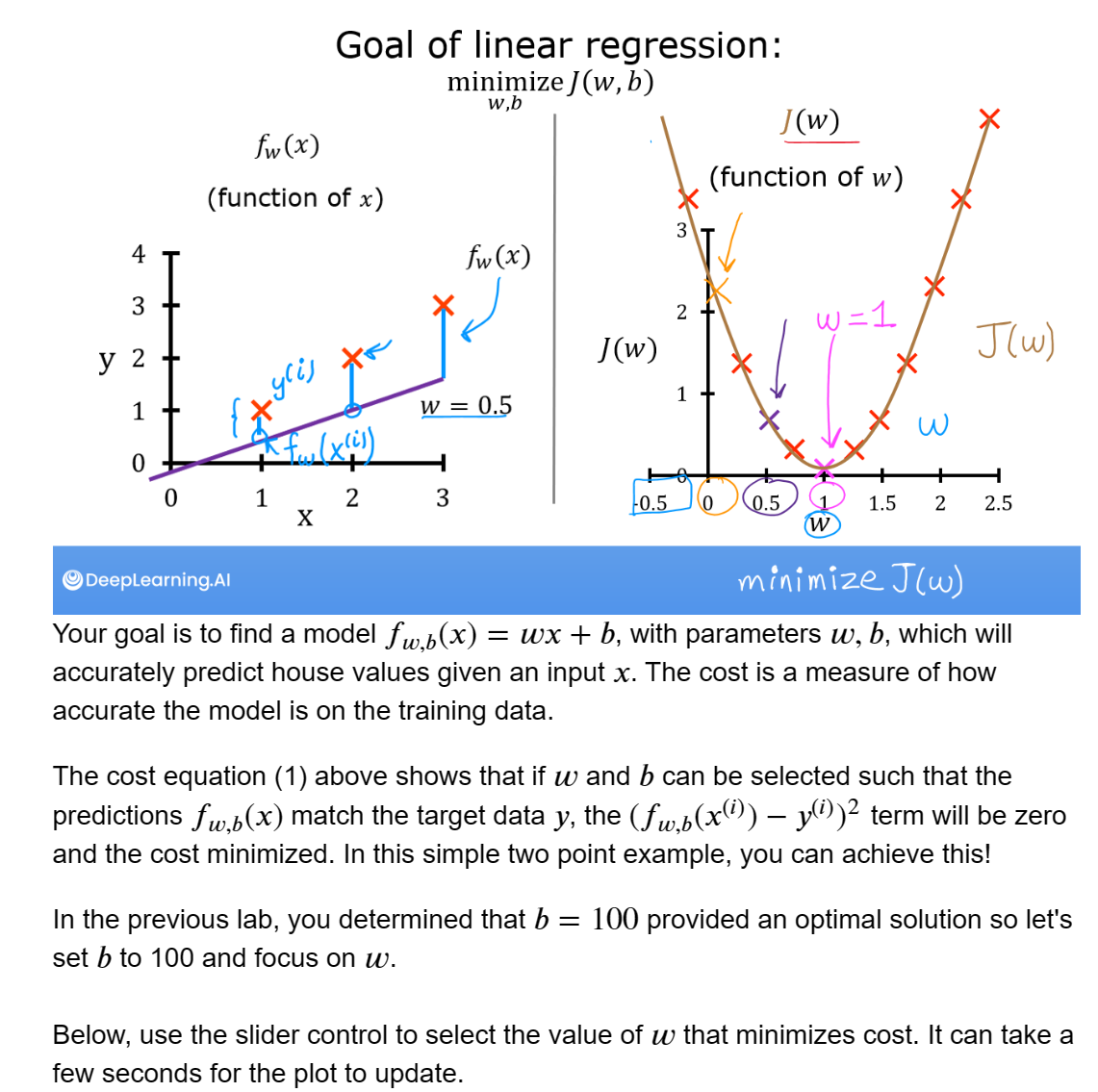
Cost Function Intuition

image-20230312172325465

1
plt_intuition(x_train, y_train)

image-20230313144221393

情节中有几点值得一提。

  • 当𝑤=200时，成本最小化，这与之前实验室的结果相吻合。
  • 因为在成本方程中，目标和预测之间的差异是平方，当𝑤时，成本迅速增加不是太大就是太小。
  • 使用通过最小化成本选择的w和b，可以得到与数据完美匹配的直线。

Cost Function Visualiztion-3D

你可以通过三维绘图或等高线图看到成本是如何随w和b变化的。

值得注意的是，这门课的一些情节会变得相当复杂。本文提供了绘图例程，虽然通读代码以熟悉这些方法是有指导意义的，但要成功完成课程并不需要这样做。例程在本地目录lab_utils_uni.py中。

Larger Data Set

较大的数据集用更多的数据点来观察一个场景是很有指导意义的。该数据集包括不在同一线上的数据点。这对成本方程意味着什么?我们能找到𝑤、𝑏那样使得代价是0?

1
2
x_train = np.array([1.0,1.7,2.0,2.5,3.0,3.2])
y_train = np.array([250,300,480,430,630,730])

在等高线图中，点击一个点，选择w和b，以达到最低的成本。使用轮廓来指导你的选择。注意，更新图形可能需要几秒钟的时间。

1
2
3
plt.close('all')
fig, ax ,dyn_items = plt_stationary(x_train, y_train)
updater = plt_update_onclick(fig, ax, x_train,y_train,dyn_items)

上面，注意左边图中的虚线。这些代表了你的训练集中每个例子所贡献的代价的部分。在本例中，值约为𝑤=209和𝑏= 2.4提供低代价。请注意，因为我们的训练示例不在一条线上，所以最小代价不为零。

Convex Cost surface

成本函数平方损失的事实确保了“误差曲面”像汤碗一样凸出。它总是有一个最小值，可以通过在所有维度上跟随梯度来达到。在前面的图中，因为𝑤和𝑏尺寸比例不同，这是不容易识别的。下图，其中𝑤和𝑏都是对称的，在讲座中展示过:

1
soup_bowl()

Congratulations!

您已经学习了以下内容:

  • 成本方程提供了一种衡量预测与训练数据匹配程度的方法。
  • 最小化成本可以提供𝑤和b的最优值。

参考资料

https://www.bilibili.com/video/BV1Pa411X76s?p=5&vd_source=3ae32e36058f58c5b85935fca9b77797

kaieye/2022-Machine-Learning-Specialization (github.com)