Computing four elements at a time

Computing four elements at a time

• 我们在子程序AddDot1x4中一次计算4个元素，该子程序一次执行4个内部乘积
• Optimization_1x4_3 · flame/how-to-optimize-gemm Wiki (github.com)
• 现在我们内联(inline)四个独立的内积，并将循环融合为一个，从而在一个循环中同时计算四个内积:
• Optimization_1x4_4 · flame/how-to-optimize-gemm Wiki (github.com)
• Optimization_1x4_5 · flame/how-to-optimize-gemm Wiki (github.com)

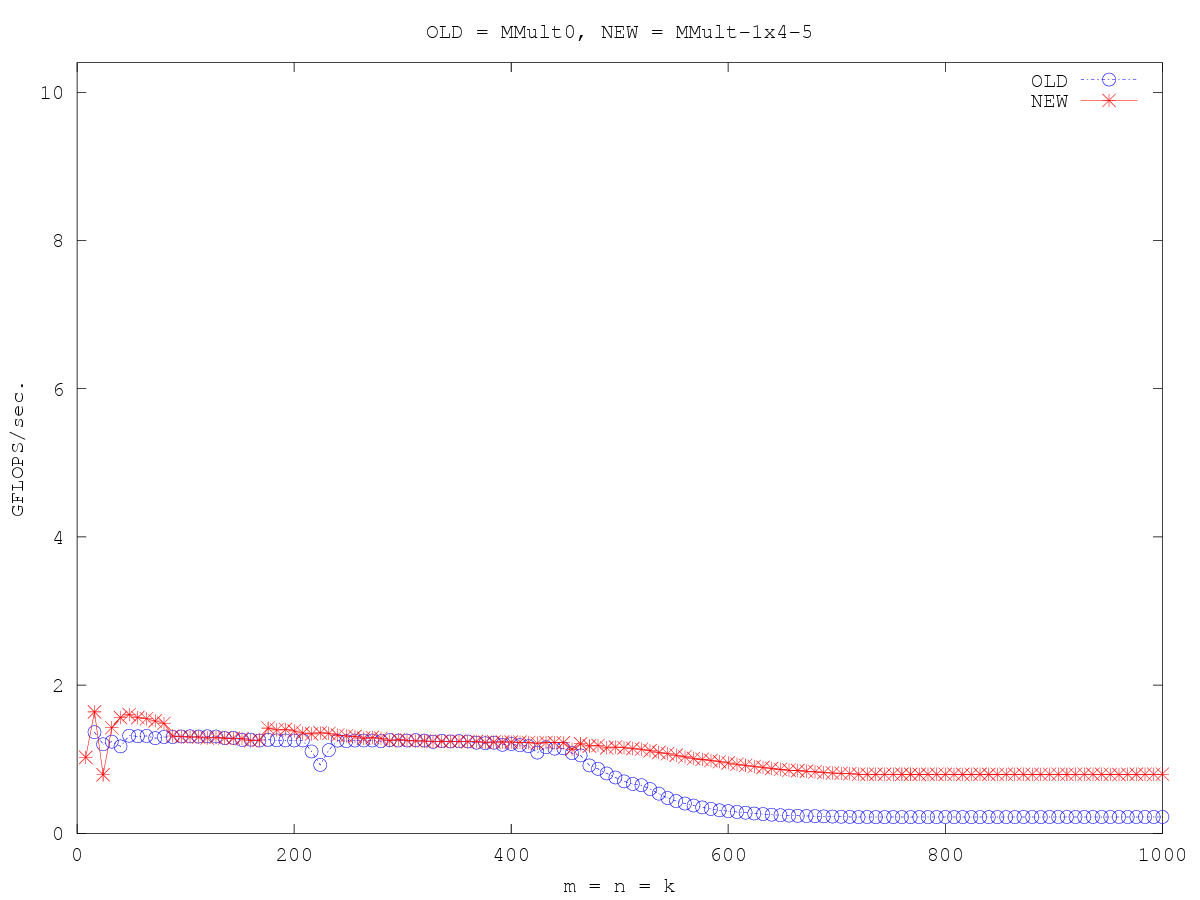
在这一点上，我们开始看到一些性能改进:

Optimization_1x4_3

/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot( int, double *, int, double *, double * );
void AddDot1x4( int, double *, int,  double *, int, double *, int )

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */
	  //相交于上个版本，把4个AddDot合并成了一个AddDot1x4
      AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot1x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes four elements of C: 

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) 
	  
     in the original matrix C */ 
  //一次AddDot1x4完成四次AddDot运算
  AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) );
  AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) );
  AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) );
  AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) );
}


/* Create macro to let X( i ) equal the ith element of x */

#define X(i) x[ (i)*incx ]

void AddDot( int k, double *x, int incx,  double *y, double *gamma )
{
  /* compute gamma := x' * y + gamma with vectors x and y of length n.

     Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1.
  */
 
  int p;

  for ( p=0; p<k; p++ ){
    *gamma += X( p ) * y[ p ];     
  }
}

Optimization_1x4_4

/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot1x4( int, double *, int,  double *, int, double *, int )

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot1x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes four elements of C: 

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) 
	  
     in the original matrix C.

     In this version, we "inline" AddDot */ 

  int p;
  //在这里我们把AddDot中的运算，全部集成到了AddDot1x4中，即4段for执行4个内部乘积
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 0 ) += A( 0, p ) * B( p, 0 );     
  }

  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 1 ) += A( 0, p ) * B( p, 1 );     
  }

  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 2 ) += A( 0, p ) * B( p, 2 );     
  }

  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 3 ) += A( 0, p ) * B( p, 3 );     
  }
}

Optimization_1x4_5

在这个版本，我们开始看到性能上的好处。原因是四个循环已经融合，因此四个内部乘积运算现在正在同时进行。这有以下好处:

• 索引p只需要每8次浮点操作更新一次(4次乘法4次加法)。
• 元素A(0, p)只需要从内存中取出一次，而不是四次。(只有当矩阵不再适合二级缓存时，这才有好处)

/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot1x4( int, double *, int,  double *, int, double *, int )

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot1x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes four elements of C: 

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) 
	  
     in the original matrix C.

     In this version, we merge the four loops, computing four inner
     products simultaneously. */

  int p;
  //在这个版本中，我们合并了4个for循环，使得可以同时计算4个乘积运算
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) );
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) );
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) );
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 0 ) += A( 0, p ) * B( p, 0 );     //第一次取A( 0, p )
    C( 0, 1 ) += A( 0, p ) * B( p, 1 );     
    C( 0, 2 ) += A( 0, p ) * B( p, 2 );     
    C( 0, 3 ) += A( 0, p ) * B( p, 3 );     
  }
}