Further optimizing

Further optimizing

对于问题大小适合L2缓存(至少部分地)有相当大的改进。不过，还有很大的改进空间。

img

Optimization_1x4_6

我们在寄存器中对当前1x4行C的更新累积，并将元素A(p, 0)放在寄存器中，以减少缓存(cache)和寄存器(reg)之间的流量(traffic)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot1x4( int, double *, int,  double *, int, double *, int )

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot1x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes four elements of C: 

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) 
	  
     in the original matrix C.

     In this version, we accumulate in registers and put A( 0, p ) in a register */

  int p;
    
    
  //C的累加在寄存器中，同时A也放在寄存器中
  register double 
    /* hold contributions to
       C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */
       c_00_reg,   c_01_reg,   c_02_reg,   c_03_reg,  
    /* holds A( 0, p ) */
       a_0p_reg;
    
  c_00_reg = 0.0; 
  c_01_reg = 0.0; 
  c_02_reg = 0.0; 
  c_03_reg = 0.0;
 
  for ( p=0; p<k; p++ ){
    a_0p_reg = A( 0, p );

    c_00_reg += a_0p_reg * B( p, 0 );     
    c_01_reg += a_0p_reg * B( p, 1 );     
    c_02_reg += a_0p_reg * B( p, 2 );     
    c_03_reg += a_0p_reg * B( p, 3 );     
  }
  //计算完成后，再通过寄存器写回C
  C( 0, 0 ) += c_00_reg; 
  C( 0, 1 ) += c_01_reg; 
  C( 0, 2 ) += c_02_reg; 
  C( 0, 3 ) += c_03_reg;
}

Optimization_1x4_7

现在使用bp0_pntr、bp1_pntr、bp2_pntr和bp3_pntr四个指针来访问元素B(p, 0)、B(p, 1)、B(p, 2)、B(p, 3)。这减少了索引开销。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot1x4( int, double *, int,  double *, int, double *, int )

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot1x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes four elements of C: 

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) 
	  
     in the original matrix C.

     In this version, we use pointer to track where in four columns of B we are */

  int p;
  register double 
    /* hold contributions to
       C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */
       c_00_reg,   c_01_reg,   c_02_reg,   c_03_reg,  
    /* holds A( 0, p ) */
       a_0p_reg;
  double 
    /* Point to the current elements in the four columns of B */
    *bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr; 
  //由于使用了宏定义，每次B(i,j)都会计算B中元素的位置
  //使用指针后，后续访问不需要再额外计算B中元素位置，只需在当前指针向后移动一位即可
  bp0_pntr = &B( 0, 0 );
  bp1_pntr = &B( 0, 1 );
  bp2_pntr = &B( 0, 2 );
  bp3_pntr = &B( 0, 3 );

  c_00_reg = 0.0; 
  c_01_reg = 0.0; 
  c_02_reg = 0.0; 
  c_03_reg = 0.0;
 
  for ( p=0; p<k; p++ ){
    a_0p_reg = A( 0, p );

    c_00_reg += a_0p_reg * *bp0_pntr++;
    c_01_reg += a_0p_reg * *bp1_pntr++;
    c_02_reg += a_0p_reg * *bp2_pntr++;
    c_03_reg += a_0p_reg * *bp3_pntr++;
  }

  C( 0, 0 ) += c_00_reg; 
  C( 0, 1 ) += c_01_reg; 
  C( 0, 2 ) += c_02_reg; 
  C( 0, 3 ) += c_03_reg;
}

Optimization_1x4_8

我们现在展开了4个循环。有趣的是，这会略微降低性能。这可能意味着，通过添加优化，我们混淆了编译器，因此它不能做以前做的优化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot1x4( int, double *, int,  double *, int, double *, int )

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot1x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes four elements of C: 

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) 
	  
     in the original matrix C.

     We now unroll the loop */

  int p;
  register double 
    /* hold contributions to
       C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */
       c_00_reg,   c_01_reg,   c_02_reg,   c_03_reg,  
    /* holds A( 0, p ) */
       a_0p_reg;
  double 
    /* Point to the current elements in the four columns of B */
    *bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr; 
    
  bp0_pntr = &B( 0, 0 );
  bp1_pntr = &B( 0, 1 );
  bp2_pntr = &B( 0, 2 );
  bp3_pntr = &B( 0, 3 );

  c_00_reg = 0.0; 
  c_01_reg = 0.0; 
  c_02_reg = 0.0; 
  c_03_reg = 0.0;
  //这里对循环变量p进行了展开，注意这里计算是顺序的
  for ( p=0; p<k; p+=4 ){
    a_0p_reg = A( 0, p );

    c_00_reg += a_0p_reg * *bp0_pntr++;
    c_01_reg += a_0p_reg * *bp1_pntr++;
    c_02_reg += a_0p_reg * *bp2_pntr++;
    c_03_reg += a_0p_reg * *bp3_pntr++;

    a_0p_reg = A( 0, p+1 );

    c_00_reg += a_0p_reg * *bp0_pntr++;
    c_01_reg += a_0p_reg * *bp1_pntr++;
    c_02_reg += a_0p_reg * *bp2_pntr++;
    c_03_reg += a_0p_reg * *bp3_pntr++;

    a_0p_reg = A( 0, p+2 );

    c_00_reg += a_0p_reg * *bp0_pntr++;
    c_01_reg += a_0p_reg * *bp1_pntr++;
    c_02_reg += a_0p_reg * *bp2_pntr++;
    c_03_reg += a_0p_reg * *bp3_pntr++;

    a_0p_reg = A( 0, p+3 );

    c_00_reg += a_0p_reg * *bp0_pntr++;
    c_01_reg += a_0p_reg * *bp1_pntr++;
    c_02_reg += a_0p_reg * *bp2_pntr++;
    c_03_reg += a_0p_reg * *bp3_pntr++;
  }

  C( 0, 0 ) += c_00_reg; 
  C( 0, 1 ) += c_01_reg; 
  C( 0, 2 ) += c_02_reg; 
  C( 0, 3 ) += c_03_reg;
}

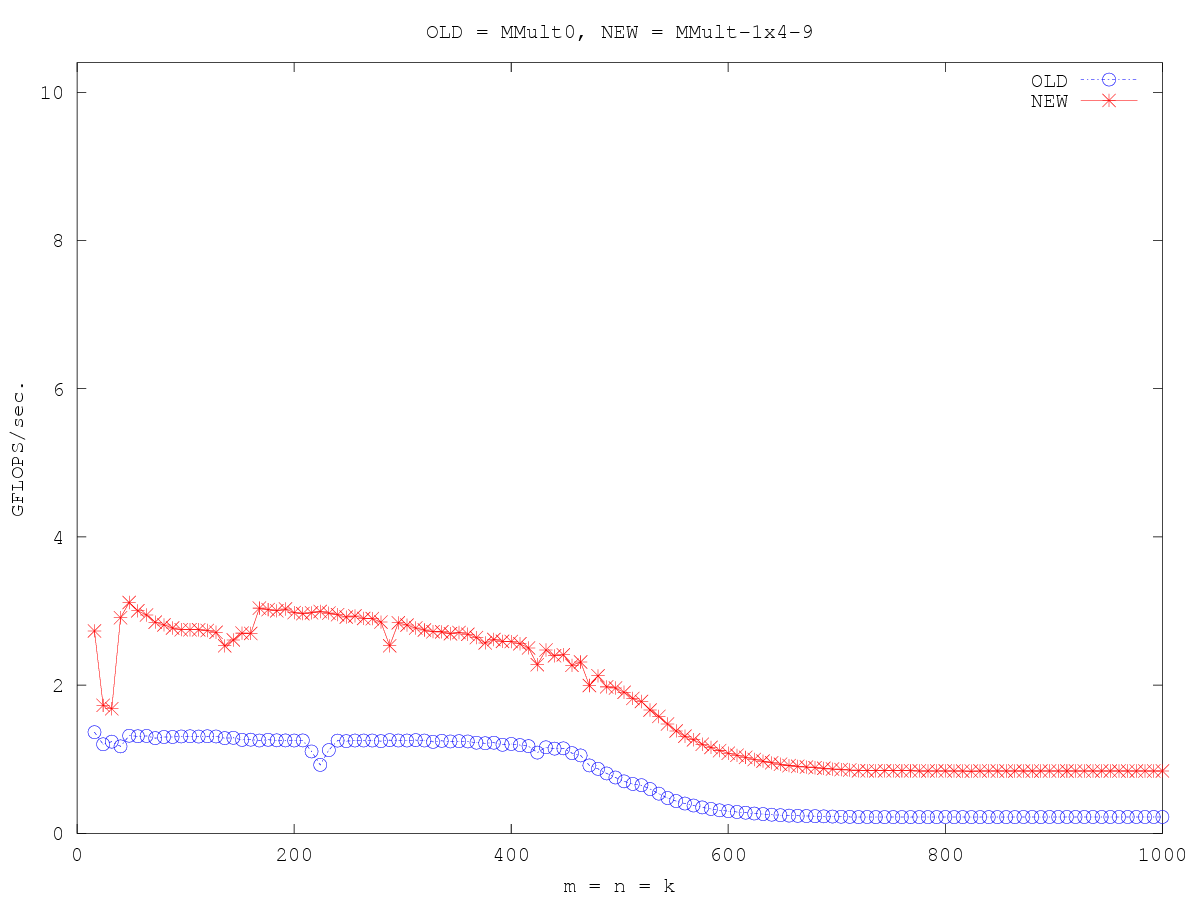
Optimization_1x4_9

在这里，*a0p_reg保存元素A(0, p+1)。

  • 我们希望bp0_pntr指向元素B（p，0）。因此，bp0_pntr+1寻址元素B（p+1，0）。有一条特殊的机器指令可以访问bp0_pntr+1处的元素，该指令不需要更新指针。

  • 因此，指向B列中元素的指针只需要在循环的第四次迭代中更新一次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot1x4( int, double *, int,  double *, int, double *, int )

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot1x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes four elements of C: 

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) 
	  
     in the original matrix C.

     We next use indirect addressing */

  int p;
  register double 
    /* hold contributions to
       C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */
       c_00_reg,   c_01_reg,   c_02_reg,   c_03_reg,  
    /* holds A( 0, p ) */
       a_0p_reg;
  double 
    /* Point to the current elements in the four columns of B */
    *bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr; 
    
  bp0_pntr = &B( 0, 0 );
  bp1_pntr = &B( 0, 1 );
  bp2_pntr = &B( 0, 2 );
  bp3_pntr = &B( 0, 3 );

  c_00_reg = 0.0; 
  c_01_reg = 0.0; 
  c_02_reg = 0.0; 
  c_03_reg = 0.0;
 
  for ( p=0; p<k; p+=4 ){
    a_0p_reg = A( 0, p );

    c_00_reg += a_0p_reg * *bp0_pntr;
    c_01_reg += a_0p_reg * *bp1_pntr;
    c_02_reg += a_0p_reg * *bp2_pntr;
    c_03_reg += a_0p_reg * *bp3_pntr;

    a_0p_reg = A( 0, p+1 );
	
    //现在我们使用间接寻址，'indirect addressing'
    c_00_reg += a_0p_reg * *(bp0_pntr+1);
    c_01_reg += a_0p_reg * *(bp1_pntr+1);
    c_02_reg += a_0p_reg * *(bp2_pntr+1);
    c_03_reg += a_0p_reg * *(bp3_pntr+1);

    a_0p_reg = A( 0, p+2 );

    c_00_reg += a_0p_reg * *(bp0_pntr+2);
    c_01_reg += a_0p_reg * *(bp1_pntr+2);
    c_02_reg += a_0p_reg * *(bp2_pntr+2);
    c_03_reg += a_0p_reg * *(bp3_pntr+2);

    a_0p_reg = A( 0, p+3 );

    c_00_reg += a_0p_reg * *(bp0_pntr+3);
    c_01_reg += a_0p_reg * *(bp1_pntr+3);
    c_02_reg += a_0p_reg * *(bp2_pntr+3);
    c_03_reg += a_0p_reg * *(bp3_pntr+3);
	
      
    //更新指针，4次迭代中仅更新一次
    bp0_pntr+=4;
    bp1_pntr+=4;
    bp2_pntr+=4;
    bp3_pntr+=4;
  }

  C( 0, 0 ) += c_00_reg; 
  C( 0, 1 ) += c_01_reg; 
  C( 0, 2 ) += c_02_reg; 
  C( 0, 3 ) += c_03_reg;
}
HPC
blas gemm gemv

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！