Repeating the same optimizations

我们在AddDot4x4子程序中一次计算4个C元素，该子程序一次执行16个乘积:
Optimization_4x4_3 · flame/how-to-optimize-gemm Wiki (github.com)
现在我们内联16个独立的内积，并将循环融合为一个，从而在一个循环中同时计算16个乘积:
Optimization_4x4_4 · flame/how-to-optimize-gemm Wiki (github.com)
Optimization_4x4_5 · flame/how-to-optimize-gemm Wiki (github.com)

在这一点上，我们再次开始看到一些性能改进:

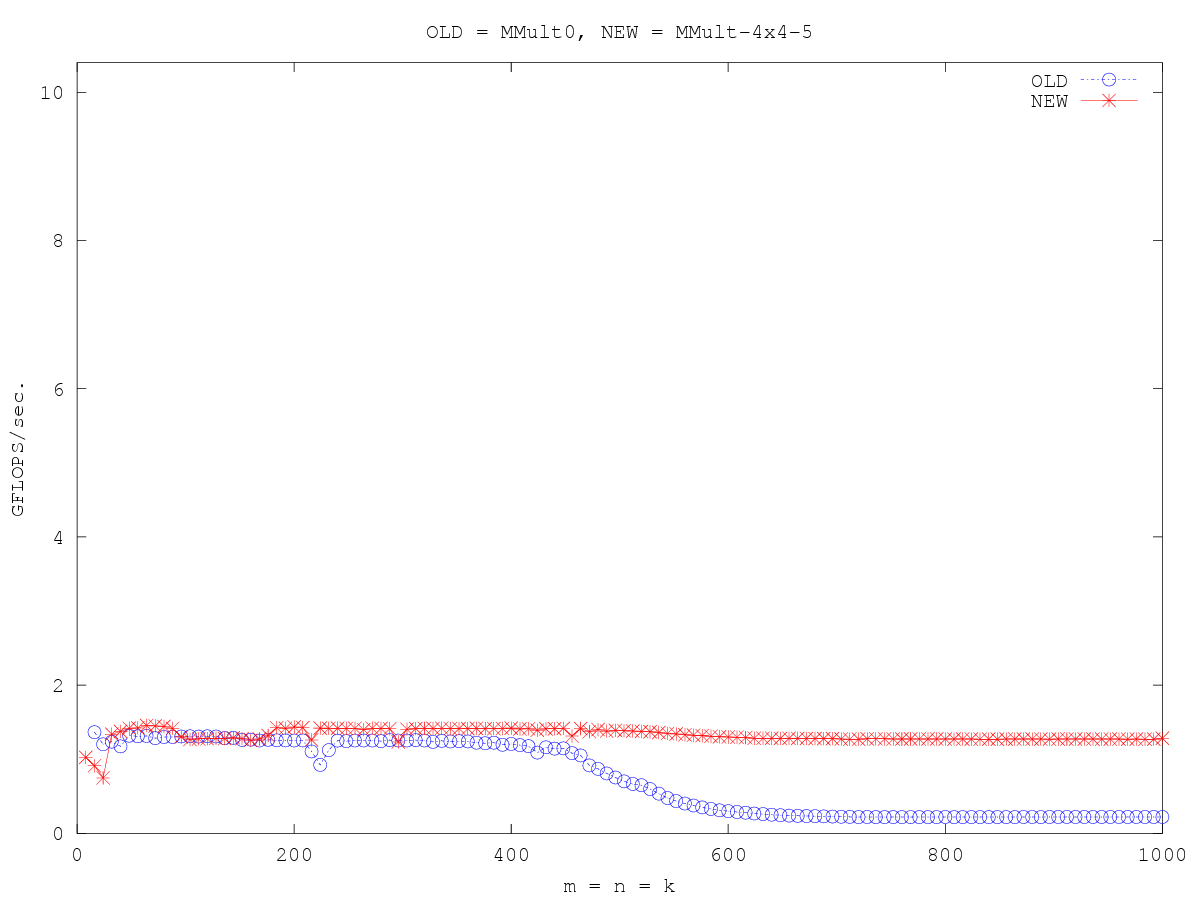
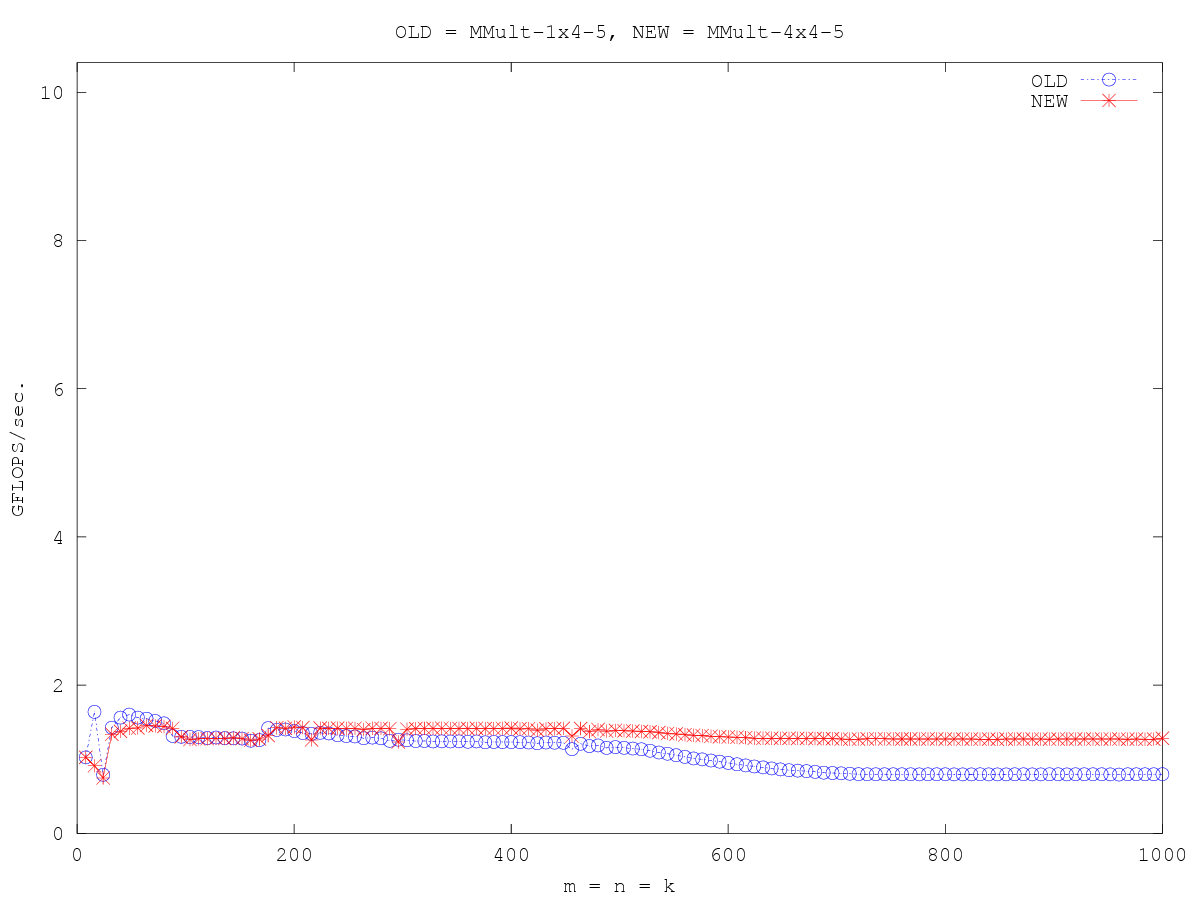
我们将C的元素累加到寄存器中，并使用寄存器存储a的元素
Optimization_4x4_6 · flame/how-to-optimize-gemm Wiki (github.com)
我们使用指针来定位B中的元素
Optimization_4x4_7 · flame/how-to-optimize-gemm Wiki (github.com)

Optimization_4x4_3

对循环变量i进行展开。由原来AddDot1x4变为AddDot4x4，一次计算16个乘积。


/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot( int, double *, int, double *, double * );

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=4 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot4x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes a 4x4 block of matrix A

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  
           C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ).  
           C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ).  
           C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i  , j ), C( i  , j+1 ), C( i  , j+2 ), C( i  , j+3 ) 
           C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) 
           C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) 
           C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) 
	  
     in the original matrix C */ 

  /* First row */
  AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) );
  AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) );
  AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) );
  AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) );

  /* Second row */
  AddDot( k, &A( 1, 0 ), lda, &B( 0, 0 ), &C( 1, 0 ) );
  AddDot( k, &A( 1, 0 ), lda, &B( 0, 1 ), &C( 1, 1 ) );
  AddDot( k, &A( 1, 0 ), lda, &B( 0, 2 ), &C( 1, 2 ) );
  AddDot( k, &A( 1, 0 ), lda, &B( 0, 3 ), &C( 1, 3 ) );

  /* Third row */
  AddDot( k, &A( 2, 0 ), lda, &B( 0, 0 ), &C( 2, 0 ) );
  AddDot( k, &A( 2, 0 ), lda, &B( 0, 1 ), &C( 2, 1 ) );
  AddDot( k, &A( 2, 0 ), lda, &B( 0, 2 ), &C( 2, 2 ) );
  AddDot( k, &A( 2, 0 ), lda, &B( 0, 3 ), &C( 2, 3 ) );

  /* Four row */
  AddDot( k, &A( 3, 0 ), lda, &B( 0, 0 ), &C( 3, 0 ) );
  AddDot( k, &A( 3, 0 ), lda, &B( 0, 1 ), &C( 3, 1 ) );
  AddDot( k, &A( 3, 0 ), lda, &B( 0, 2 ), &C( 3, 2 ) );
  AddDot( k, &A( 3, 0 ), lda, &B( 0, 3 ), &C( 3, 3 ) );
}


/* Create macro to let X( i ) equal the ith element of x */

#define X(i) x[ (i)*incx ]

void AddDot( int k, double *x, int incx,  double *y, double *gamma )
{
  /* compute gamma := x' * y + gamma with vectors x and y of length n.

     Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1.
  */
 
  int p;

  for ( p=0; p<k; p++ ){
    *gamma += X( p ) * y[ p ];     
  }
}

Optimization_4x4_4

把AddDot计算kernel合并到AddDot4x4里面。


/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot4x4( int, double *, int, double *, int, double *, int );
void AddDot( int, double *, int, double *, double * );

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=4 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot4x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes a 4x4 block of matrix A

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  
           C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ).  
           C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ).  
           C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i  , j ), C( i  , j+1 ), C( i  , j+2 ), C( i  , j+3 ) 
           C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) 
           C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) 
           C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) 
	  
     in the original matrix C 

     In this version, we "inline" AddDot */ 

  int p;

  /* First row 第一行*/   
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 0 ) += A( 0, p ) * B( p, 0 );     
  }
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 1 ) += A( 0, p ) * B( p, 1 );     
  }
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 2 ) += A( 0, p ) * B( p, 2 );     
  }
  //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) );
  for ( p=0; p<k; p++ ){
    C( 0, 3 ) += A( 0, p ) * B( p, 3 );     
  }

  /* Second row 第二行*/
  //  AddDot( k, &A( 1, 0 ), lda, &B( 0, 0 ), &C( 1, 0 ) );
  for ( p=0; p<k; p++ ){
    C( 1, 0 ) += A( 1, p ) * B( p, 0 );     
  }
  //  AddDot( k, &A( 1, 0 ), lda, &B( 0, 1 ), &C( 1, 1 ) );
  for ( p=0; p<k; p++ ){
    C( 1, 1 ) += A( 1, p ) * B( p, 1 );     
  }
  //  AddDot( k, &A( 1, 0 ), lda, &B( 0, 2 ), &C( 1, 2 ) );
  for ( p=0; p<k; p++ ){
    C( 1, 2 ) += A( 1, p ) * B( p, 2 );     
  }
  //  AddDot( k, &A( 1, 0 ), lda, &B( 0, 3 ), &C( 1, 3 ) );
  for ( p=0; p<k; p++ ){
    C( 1, 3 ) += A( 1, p ) * B( p, 3 );     
  }

  /* Third row 第三行*/
  //  AddDot( k, &A( 2, 0 ), lda, &B( 0, 0 ), &C( 2, 0 ) );
  for ( p=0; p<k; p++ ){
    C( 2, 0 ) += A( 2, p ) * B( p, 0 );     
  }
  //  AddDot( k, &A( 2, 0 ), lda, &B( 0, 1 ), &C( 2, 1 ) );
  for ( p=0; p<k; p++ ){
    C( 2, 1 ) += A( 2, p ) * B( p, 1 );     
  }
  //  AddDot( k, &A( 2, 0 ), lda, &B( 0, 2 ), &C( 2, 2 ) );
  for ( p=0; p<k; p++ ){
    C( 2, 2 ) += A( 2, p ) * B( p, 2 );     
  }
  //  AddDot( k, &A( 2, 0 ), lda, &B( 0, 3 ), &C( 2, 3 ) );
  for ( p=0; p<k; p++ ){
    C( 2, 3 ) += A( 2, p ) * B( p, 3 );     
  }

  /* Four row 第四行*/
  //  AddDot( k, &A( 3, 0 ), lda, &B( 0, 0 ), &C( 3, 0 ) );
  for ( p=0; p<k; p++ ){
    C( 3, 0 ) += A( 3, p ) * B( p, 0 );     
  }
  //  AddDot( k, &A( 3, 0 ), lda, &B( 0, 1 ), &C( 3, 1 ) );
  for ( p=0; p<k; p++ ){
    C( 3, 1 ) += A( 3, p ) * B( p, 1 );     
  }
  //  AddDot( k, &A( 3, 0 ), lda, &B( 0, 2 ), &C( 3, 2 ) );
  for ( p=0; p<k; p++ ){
    C( 3, 2 ) += A( 3, p ) * B( p, 2 );     
  }
  //  AddDot( k, &A( 3, 0 ), lda, &B( 0, 3 ), &C( 3, 3 ) );
  for ( p=0; p<k; p++ ){
    C( 3, 3 ) += A( 3, p ) * B( p, 3 );     
  }
}

Optimization_4x4_5

合并16个for循环。

现在，当矩阵变大时，我们看到了性能上的好处，因为数据在被放入寄存器后会得到更多的重用。

以前是：1x4_5(一次计算C的4个元素)现在是：4x4_5(一次计算C的16个元素)。


/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot4x4( int, double *, int, double *, int, double *, int );
void AddDot( int, double *, int, double *, double * );

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=4 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot4x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes a 4x4 block of matrix A

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  
           C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ).  
           C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ).  
           C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i  , j ), C( i  , j+1 ), C( i  , j+2 ), C( i  , j+3 ) 
           C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) 
           C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) 
           C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) 
	  
     in the original matrix C 

     In this version, we merge each set of four loops, computing four
     inner products simultaneously. */

  int p;

  for ( p=0; p<k; p++ ){
    /* First row */
    C( 0, 0 ) += A( 0, p ) * B( p, 0 );     
    C( 0, 1 ) += A( 0, p ) * B( p, 1 );     
    C( 0, 2 ) += A( 0, p ) * B( p, 2 );     
    C( 0, 3 ) += A( 0, p ) * B( p, 3 );     

    /* Second row */
    C( 1, 0 ) += A( 1, p ) * B( p, 0 );     
    C( 1, 1 ) += A( 1, p ) * B( p, 1 );     
    C( 1, 2 ) += A( 1, p ) * B( p, 2 );     
    C( 1, 3 ) += A( 1, p ) * B( p, 3 );     

    /* Third row */
    C( 2, 0 ) += A( 2, p ) * B( p, 0 );     
    C( 2, 1 ) += A( 2, p ) * B( p, 1 );     
    C( 2, 2 ) += A( 2, p ) * B( p, 2 );     
    C( 2, 3 ) += A( 2, p ) * B( p, 3 );     

    /* Fourth row */
    C( 3, 0 ) += A( 3, p ) * B( p, 0 );     
    C( 3, 1 ) += A( 3, p ) * B( p, 1 );     
    C( 3, 2 ) += A( 3, p ) * B( p, 2 );     
    C( 3, 3 ) += A( 3, p ) * B( p, 3 );     
  }
}

Optimization_4x4_6

矩阵C和A采用寄存器来存。

我们为C的4x4块和A的当前4x1列的元素使用(常规)寄存器，这一事实使性能受益。请注意，我们使用的是比实际存在的更多的常规寄存器，所以任何人都可以猜测编译器会用它做什么。


/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot4x4( int, double *, int, double *, int, double *, int );

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=4 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot4x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes a 4x4 block of matrix A

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  
           C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ).  
           C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ).  
           C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i  , j ), C( i  , j+1 ), C( i  , j+2 ), C( i  , j+3 ) 
           C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) 
           C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) 
           C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) 
	  
     in the original matrix C 

     In this version, we accumulate in registers and put A( 0, p ) in a register */

  int p;
  register double 
    /* hold contributions to
       C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) 
       C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ) 
       C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ) 
       C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 )   */
       c_00_reg,   c_01_reg,   c_02_reg,   c_03_reg,  
       c_10_reg,   c_11_reg,   c_12_reg,   c_13_reg,  
       c_20_reg,   c_21_reg,   c_22_reg,   c_23_reg,  
       c_30_reg,   c_31_reg,   c_32_reg,   c_33_reg,
    /* hold 
       A( 0, p ) 
       A( 1, p ) 
       A( 2, p ) 
       A( 3, p ) */
       a_0p_reg,
       a_1p_reg,
       a_2p_reg,
       a_3p_reg;

  c_00_reg = 0.0;   c_01_reg = 0.0;   c_02_reg = 0.0;   c_03_reg = 0.0;
  c_10_reg = 0.0;   c_11_reg = 0.0;   c_12_reg = 0.0;   c_13_reg = 0.0;
  c_20_reg = 0.0;   c_21_reg = 0.0;   c_22_reg = 0.0;   c_23_reg = 0.0;
  c_30_reg = 0.0;   c_31_reg = 0.0;   c_32_reg = 0.0;   c_33_reg = 0.0;

  for ( p=0; p<k; p++ ){
    a_0p_reg = A( 0, p );
    a_1p_reg = A( 1, p );
    a_2p_reg = A( 2, p );
    a_3p_reg = A( 3, p );

    /* First row */
    c_00_reg += a_0p_reg * B( p, 0 );     
    c_01_reg += a_0p_reg * B( p, 1 );     
    c_02_reg += a_0p_reg * B( p, 2 );     
    c_03_reg += a_0p_reg * B( p, 3 );     

    /* Second row */
    c_10_reg += a_1p_reg * B( p, 0 );     
    c_11_reg += a_1p_reg * B( p, 1 );     
    c_12_reg += a_1p_reg * B( p, 2 );     
    c_13_reg += a_1p_reg * B( p, 3 );     

    /* Third row */
    c_20_reg += a_2p_reg * B( p, 0 );     
    c_21_reg += a_2p_reg * B( p, 1 );     
    c_22_reg += a_2p_reg * B( p, 2 );     
    c_23_reg += a_2p_reg * B( p, 3 );     

    /* Four row */
    c_30_reg += a_3p_reg * B( p, 0 );     
    c_31_reg += a_3p_reg * B( p, 1 );     
    c_32_reg += a_3p_reg * B( p, 2 );     
    c_33_reg += a_3p_reg * B( p, 3 );     
  }

  C( 0, 0 ) += c_00_reg;   C( 0, 1 ) += c_01_reg;   C( 0, 2 ) += c_02_reg;   C( 0, 3 ) += c_03_reg;
  C( 1, 0 ) += c_10_reg;   C( 1, 1 ) += c_11_reg;   C( 1, 2 ) += c_12_reg;   C( 1, 3 ) += c_13_reg;
  C( 2, 0 ) += c_20_reg;   C( 2, 1 ) += c_21_reg;   C( 2, 2 ) += c_22_reg;   C( 2, 3 ) += c_23_reg;
  C( 3, 0 ) += c_30_reg;   C( 3, 1 ) += c_31_reg;   C( 3, 2 ) += c_32_reg;   C( 3, 3 ) += c_33_reg;
}

Optimization_4x4_7

这里我们改为使用指针来跟踪B的当前4x1块。


/* Create macros so that the matrices are stored in column-major order */

#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

/* Routine for computing C = A * B + C */

void AddDot4x4( int, double *, int, double *, int, double *, int );

void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=4 ){        /* Loop over the rows of C */
      /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
	 one routine (four inner products) */

      AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
    }
  }
}


void AddDot4x4( int k, double *a, int lda,  double *b, int ldb, double *c, int ldc )
{
  /* So, this routine computes a 4x4 block of matrix A

           C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).  
           C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ).  
           C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ).  
           C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ).  

     Notice that this routine is called with c = C( i, j ) in the
     previous routine, so these are actually the elements 

           C( i  , j ), C( i  , j+1 ), C( i  , j+2 ), C( i  , j+3 ) 
           C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) 
           C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) 
           C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) 
	  
     in the original matrix C 

     In this version, we use pointer to track where in four columns of B we are */

  int p;
  register double 
    /* hold contributions to
       C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) 
       C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ) 
       C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ) 
       C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 )   */
       c_00_reg,   c_01_reg,   c_02_reg,   c_03_reg,  
       c_10_reg,   c_11_reg,   c_12_reg,   c_13_reg,  
       c_20_reg,   c_21_reg,   c_22_reg,   c_23_reg,  
       c_30_reg,   c_31_reg,   c_32_reg,   c_33_reg,
    /* hold 
       A( 0, p ) 
       A( 1, p ) 
       A( 2, p ) 
       A( 3, p ) */
       a_0p_reg,
       a_1p_reg,
       a_2p_reg,
       a_3p_reg;
  double 
    /* Point to the current elements in the four columns of B */
    *b_p0_pntr, *b_p1_pntr, *b_p2_pntr, *b_p3_pntr; 

  c_00_reg = 0.0;   c_01_reg = 0.0;   c_02_reg = 0.0;   c_03_reg = 0.0;
  c_10_reg = 0.0;   c_11_reg = 0.0;   c_12_reg = 0.0;   c_13_reg = 0.0;
  c_20_reg = 0.0;   c_21_reg = 0.0;   c_22_reg = 0.0;   c_23_reg = 0.0;
  c_30_reg = 0.0;   c_31_reg = 0.0;   c_32_reg = 0.0;   c_33_reg = 0.0;

  for ( p=0; p<k; p++ ){
    a_0p_reg = A( 0, p );
    a_1p_reg = A( 1, p );
    a_2p_reg = A( 2, p );
    a_3p_reg = A( 3, p );
	  
    b_p0_pntr = &B( p, 0 );
    b_p1_pntr = &B( p, 1 );
    b_p2_pntr = &B( p, 2 );
    b_p3_pntr = &B( p, 3 );	  

    /* First row */
    c_00_reg += a_0p_reg * *b_p0_pntr;     
    c_01_reg += a_0p_reg * *b_p1_pntr;     
    c_02_reg += a_0p_reg * *b_p2_pntr;     
    c_03_reg += a_0p_reg * *b_p3_pntr;     

    /* Second row */
    c_10_reg += a_1p_reg * *b_p0_pntr;     
    c_11_reg += a_1p_reg * *b_p1_pntr;     
    c_12_reg += a_1p_reg * *b_p2_pntr;     
    c_13_reg += a_1p_reg * *b_p3_pntr;     

    /* Third row */
    c_20_reg += a_2p_reg * *b_p0_pntr;     
    c_21_reg += a_2p_reg * *b_p1_pntr;     
    c_22_reg += a_2p_reg * *b_p2_pntr;     
    c_23_reg += a_2p_reg * *b_p3_pntr;     

    /* Four row */
    c_30_reg += a_3p_reg * *b_p0_pntr++;     
    c_31_reg += a_3p_reg * *b_p1_pntr++;     
    c_32_reg += a_3p_reg * *b_p2_pntr++;     
    c_33_reg += a_3p_reg * *b_p3_pntr++;     
  }

  C( 0, 0 ) += c_00_reg;   C( 0, 1 ) += c_01_reg;   C( 0, 2 ) += c_02_reg;   C( 0, 3 ) += c_03_reg;
  C( 1, 0 ) += c_10_reg;   C( 1, 1 ) += c_11_reg;   C( 1, 2 ) += c_12_reg;   C( 1, 3 ) += c_13_reg;
  C( 2, 0 ) += c_20_reg;   C( 2, 1 ) += c_21_reg;   C( 2, 2 ) += c_22_reg;   C( 2, 3 ) += c_23_reg;
  C( 3, 0 ) += c_30_reg;   C( 3, 1 ) += c_31_reg;   C( 3, 2 ) += c_32_reg;   C( 3, 3 ) += c_33_reg;
}

HPC

blas gemm gemv

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

Further optimizing 上一篇

Further optimizing 下一篇